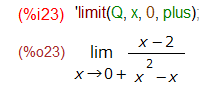前回までで線形代数の教科書1冊の練習完了(練習したのはMaxima様で、私は身についていないケド)。今回より微積分の練習に入ります。微積といえば、最初に登場するのは極限ですな。以前に一度やっておるのでありますが忘却の彼方。あれれ、右方極限とか左方極限とかどうやって計算(Maxima様にお願い)するのだったっけ?
※「忘却の微分方程式」投稿順 index はこちら
今回より読ませていただくのは以下の教科書(参考書、問題集?)であります。
予備校の先生がお書きになっている御本なのでとっても分かり易いです(個人の感想です。)私が大学生だったころ(大昔だ)にこういう御本があったら良かった。
参照しているMaximaマニュアル(日本語)
極限関係の関数のマニュアルは以下です。
上記から大事なところを1か所引用させていただきます。
limitは以下の特殊シンボルを使います: inf (正の無限大)と minf (負の無限大) 出力時には und (未定義), ind (不定しかし有界), infinity (複素無限大)も使うことがあります。
今回は、あまり見たくもない「特殊シンボル」を目にせざるを得ないので上記をおぼえていないと、ビビること必定。
limit()の使い方を思い出す
limit求めるのは以下の回で一度やってます。
忘却の微分方程式(23) 極限(limit)、MathematicaとMaxima
といいつつ圧倒的な忘却力にて、老人なにも覚えてません。しかし、寛大なMaxima様にはお助けコマンドがいくつかありませす。今回は、example()にお願いしてみました。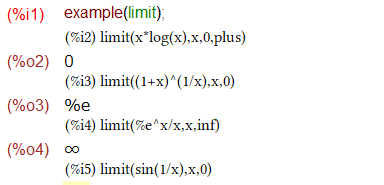
limit()関数の使い方、何となく思い出したような気がするので、先に進みます。まあ、クラッシュしたら、その時考えれば良いと。いい加減だな。
右方極限、左方極限、再び
冒頭のアイキャッチ画像に最初の問題を limitの形で表示しました。しかし、毎回、数学的に綺麗に書き直しているとメンドイので、素っ気ないスタイルで進めます。
最初の例題の極限は、左右とか指定せずにただ x → 0 で極限を求めようとすると infinity が返ってきます。先ほどの引用を思い出すと infinity=複素無限大です。これまた意味がサッパリ?
しかし、plus方向から右方極限、minus方向から左方極限もとめるとその意味はハッキリします。そういうことね。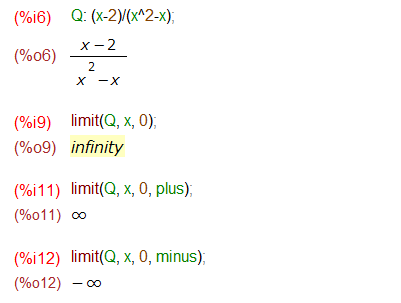
右と左が一致しないので、極限 x → 0 は存在しないっと。
次の例題は und が返ってきます。und=未定義とな。これまた、左右の極限を求めてみるとハッキリします。0と1、そこには深い断絶があったと。知らんけど。
ということで、これまた極限 x → 0 は存在しないっと。
不定形
教科書では、不定形 0/0、無限大-無限大などが現れる場合の処理のコツを形ごとに分類してお教えいただいておるのです。しかしこちらはMaxima様にお願いするのみ。
例題はこんな感じ。自分じゃ絶対解きたくないデス(多分、確実に途中で計算間違えます。)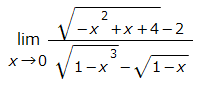
しかし、Maxima様にお願いする分には簡単、ここでは右も左もありゃしません。解けます。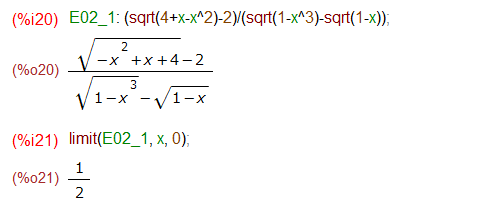
※計算せず、limの形式で表示を止めときたい場合は、シングルクウォートを頭につけます。