
前回は直交信号発生器でした。今回メインはダウン・サンプラです。しかし、ここで前々回「やった」CICフィルタが再登場します。CICフィルタを積分器部分と櫛型フィルタ部分に分け、その中間にダウンサンプラを組み込むことで櫛型フィルタ部分を一挙に簡単化するという大技を繰り出すためです。この定番を最初に考えついた人は誰なのかな?
※「手習ひデジタル信号処理」投稿順 Indexはこちら
※教科書として読ませていただいておりますのは、以下の三上先生の御本です。
CQ出版社『Armマイコンでつくるダイレクト・サンプリングSDR』
元記事はCQ出版社トラ技誌の2021年連載です。上記はそれをまとめたPDF版のダウンロードサイトへのリンクです。
ダウンサンプリングの前にLPF
今回は、上記教科書の第3回の中盤に入りました。アンダーサンプリング後の信号に直交信号発生器で生成したCOS波SIN波を乗じて得た信号をCICフィルタを使ったダウンサンプリングでサンプリング周波数を落としていく部分です。
COS側とSIN側と信号は2つあります。片側の基本的構成が以下のブロックダイアグラムに。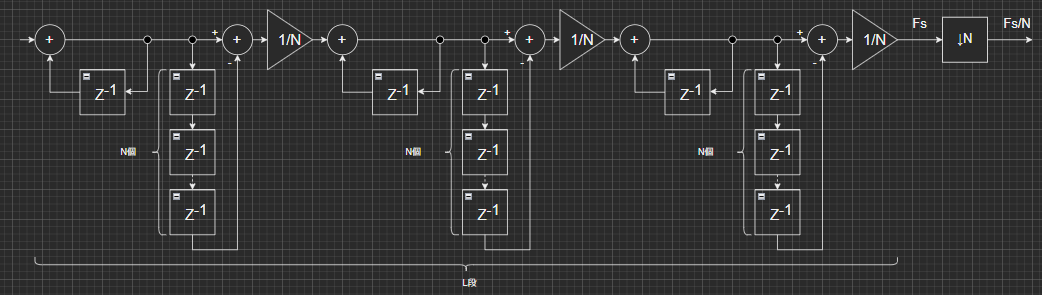
上記では、CICフィルタを3段重ねて接続しとります。これは1段では高域の減衰量が十分でないためです。基本構成では、CICフィルタの後に1/Nのダウンサンプラを接続するかたちです。ダウンサンプラはN回に1個だけサンプルを通すだけなので、実装は簡単じゃないかと思います。知らんけど。
以下にCICフィルタを1段、2段、3段(L)と接続したときのゲインの様子をScilabで計算するためのスクリプトを掲げました。前々回のもののチョイ直しであります。
clc;
clear();
clf();
M=10
L=1
Hz1 = syslin('d', ((1/M)*(1-%z^(-M))/(1-%z^-1))^L)
L=2
Hz2 = syslin('d', ((1/M)*(1-%z^(-M))/(1-%z^-1))^L)
L=3
Hz3 = syslin('d', ((1/M)*(1-%z^(-M))/(1-%z^-1))^L)
gainplot([Hz1; Hz2; Hz3], 0.01, 0.5)
hl=legend(['L=1','L=2','L=3'],3)
xtitle("多段CIC Filter L=1,2,3 正規化周波数 Gain Plot")
上記を実行して得た特性が以下に。教科書では第3回の図5のグラフに対応するものです。教科書の方はX軸がリニア、こちらは対数、教科書はL=4段まであり、こちらは3段と微妙に違います。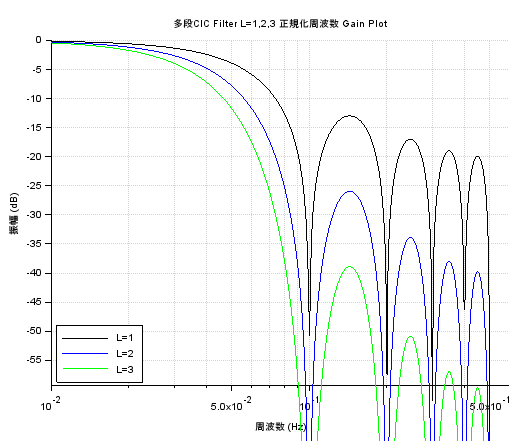
積分器+ダウンサンプラ+櫛型フィルタ
私は不勉強なのでどこのどなたが発明されたのかは存じ上げないのでありますが、ダウンサンプラのど定番、CICフィルタの前後を分離して積分器と櫛型フィルタの間にダウンサンプラを組み込むことで、後段の櫛型フィルタの遅延器の数をバッサリという構成が以下です。
ブロックダイアグラムが以下に。
今回はCICフィルタ+ダウンサンプラでしたが、この先もう一段、FIRフィルタ+ダウンサンプラが登場する筈。これにてAMラジオのサウンサンプリングが完了とな?
