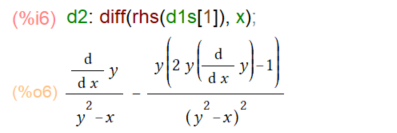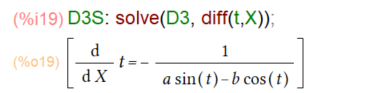前々回は陰関数を微分、前回は媒介変数表示の関数を微分でした。今回は2階の微分なのですが、単純な関数を2階微分するのは芸がないということか、2階の微分の対象は陰関数と媒介変数表示の関数です。Maxima様が計算してくれるのですが正直メンドイです。まあ、高次といっても2階微分できればだいたいの工学的な問題はオッケー?
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の教科書(参考書、問題集?)の例題をMaximaの練習に使わせていただいております。
大昔、大学生のときにこういう御本が欲しかったです。
※以下のMaxima/wxMaximaバージョンで実習させていただいております。
-
- Maxima 5.46.0
- wxMaxima 22.04.0
陰関数の2階微分
単純な関数、たとえばy=x^3などであれば、diff()関数の第2引数に2階微分の2を指定すれば 6x と答えが求まります。下は「形」だけですけれども。
しかし、以下の f0=0 のような陰関数ではどうよ、と。
前々回やったとおり、まずは depends()で、yがxの関数なのよ、と宣言しておきます。そのうえで正面突破、f0をまずは1階微分、さらにもう1階と微分していくことにいたします。1階の微分が以下に。
微分結果のd1が例によって整理されていなかったので、上記のようにsolveを使ってdy/dx=の形に整理いたしました。solveのせいで式がリストの中にくるまれているので注意しないとなりまへん。
そして1階微分の結果d1sの右辺rhs(リストd1sの第1要素)を、xで微分すれば2階微分となる、と。こんな感じ。
一応2階微分できたのですが、その中にはdy/dxが含まれております。しかしこれはd1sですでに求まっているので、subst使って置き換えてやりました。結果は一瞬複雑になりましたが、factor()一発、人間が望む形のお答えとなりましたです。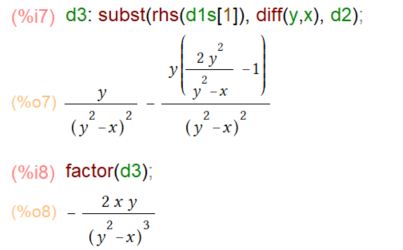
なんとか様になってよかった。
媒介変数表示された関数の2階微分
前回、媒介変数表示された関数の微分の「公式」的なものを掲げましたが、今回はそれをさらにもう1階微分した場合です。こんな感じ。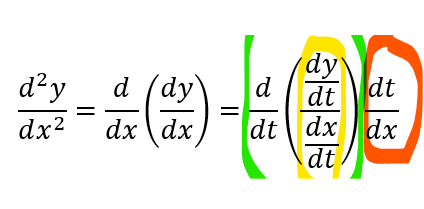
手順としては、
-
- 前回の1階微分の部分(黄色)をまず求める
- 黄色をtでもう一回微分
- それに赤の部分の微分を乗ずる
前回、最初のステップだけでもメンドかったのに、3回とな。
まずは、媒介変数で変数 xf と yf を定義したものが以下に。これを2階微分せよ、ということであります。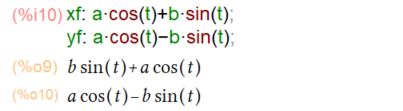
第1ステップ、黄色の部分。xf, yfをまずはtで微分し、その結果を組み合わせて黄色を求めると。
上記までは前回やった通りです。
さらに上記の結果を、tで微分してやると上の公式の緑の部分が求まるハズ。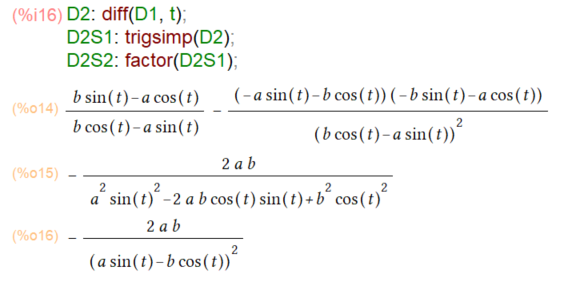
例によって、微分直後は、見たくもない複雑な形がボロリンと提示されますが、Maxima様にはtrigsimp(), factor()といった式を変形するための「お道具」がそろっているので、上記のように整理できました。そこそこいい感じ?
一方赤の部分は、xf=Xとおいた式の t がXの関数だと思って微分せにゃなりません。dependsでその関係を定義し、Xで微分すると以下のようです。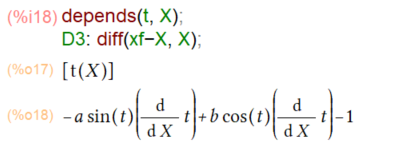
上記のリストの第1要素の右辺をとれば、赤の部分も求まったと。
最後、緑の結果 D2S2と赤の部分を掛け算すれば、2階微分の答えが求まるハズ。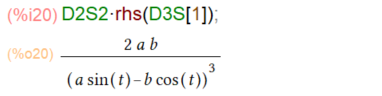
いや~、メンドい(実際に計算したのはMaxima様だけれども。)でもお答えはあっているみたい。