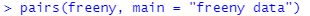前回は「構造をもった」データセットでロード時と使用時でお名前が違いフェイント気味でした。今回も内部に構造をもったデータセットなのですが、ロードも使用もすんなりです。この辺の作り方にいろいろ流派があるのかも知れないです。でもコマケー話にガタガタ言うなとか言われそう。中を見れば分かる、と。
※「データのお砂場」投稿順Indexはこちら
今回のサンプルデータセット
R言語に付属しているデータセットをアルファベット順、ただし大文字始まりは一巡、現在は小文字始まりを経めぐっております。今回は Freeny という名のサンプルデータセットです。
サンプルデータセットのリストの上では以下のように3行に分かれて見えるのですが、1個のデータセットです。
今回のサンプルデータセットの解説ページは以下にあります。
お名前からすると 「Freenyさん?の収入データ」ってことかい。データのソースがFreenyという名のベル研の人がかかれたものだからみたいです。サンプルデータセットの意図としては、重回帰分析をせよ、ということみたい。
内部には、1962年のQ2から1971年の4Qにいたる4半期Revenueの時系列データ(被説明変数)と、説明変数として以下の4つを並べた配列が格納されております。
-
- lag.quarterly.revenue revenueの数字を4半期遅らせた(lag)もの
- price.index 物価指数?
- income.level 収入のレベル?
- market.potential 市場ポテンシャル?
だいたい revenueの単位からして不明、上記の説明変数もlag以外の素性はなんだかまったく不明であります。コマケー話に気をそらせずに、目の前の抽象的な数字に向き合え、ってことですかい。
なお時系列データは freeny.y、説明変数の配列の方は freeny.xというお名前でも参照することができます。
今回は重回帰分析ということで、以下のページを参照させていただきました。ありがとうございます。
まずは生データ
data("freeny")
とやって、freenyをロード後、まずはその構造を観察したところが以下に。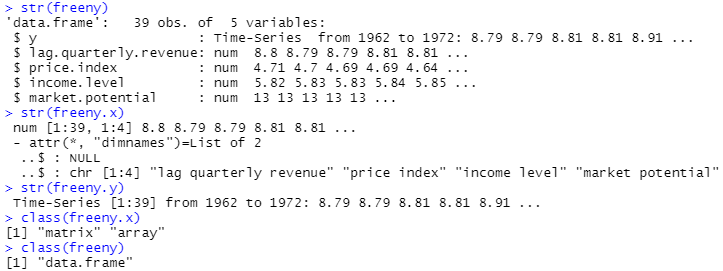
freenyの全体は、data.frameであり、その中にfreeny.y に説明変数の時系列データが、freeny.xに被説明変数の配列が含まれているという構造であります。
サンプル処理にそって
さきほどのデータセット解説ページには、サンプル処理例が掲載されているので、今回はそれにそって処理してお茶をにごしますです。まずは全貌をsummaryで見てみる、と。
最大、最小、平均、中央値などわかりますが、どういう素性の数値でどういう単位なのかも不明、具象に引きずられ、抽象世界に専念できない頭の固い年寄にはイメージが膨らみませぬ。
さて続いてはプロットですが、使用するのは pairs です。上記の5つの変数間の
スキャッタプロット をマトリックス状にプロットするもの。コマンドは以下に。
右肩あがりと、右肩さがりで、ほぼほぼ直線的な関係が描かれております。これは線形な回帰式で良いんでないかい、とこの統計素人にも分かりますな。
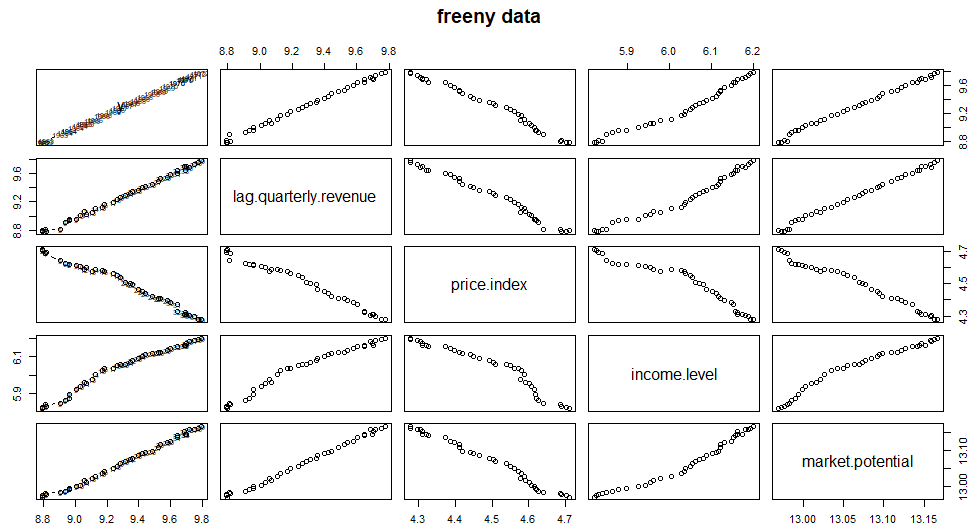
「線形」な回帰、ただし説明変数は4つある、ので重回帰です。線形なlm()関数で計算してもらいます。被説明変数は y、説明変数のところにある「.」は data=freenyの中の「被説明変数以外の全ての変数を説明変数として用いる」ということみたいっす。計算結果のサマリが以下に
上記で、黄色くマーカ引いておきましたが、price.indexとincome.levelとは無関係という帰無仮説は有意に棄却できるんでないかと。知らんけど。まあpriceが上昇するとRevenueが低下し、incomeがあがるとRevenueも上昇するという傾向。当たり前にも思えますが、1960年代は健全?
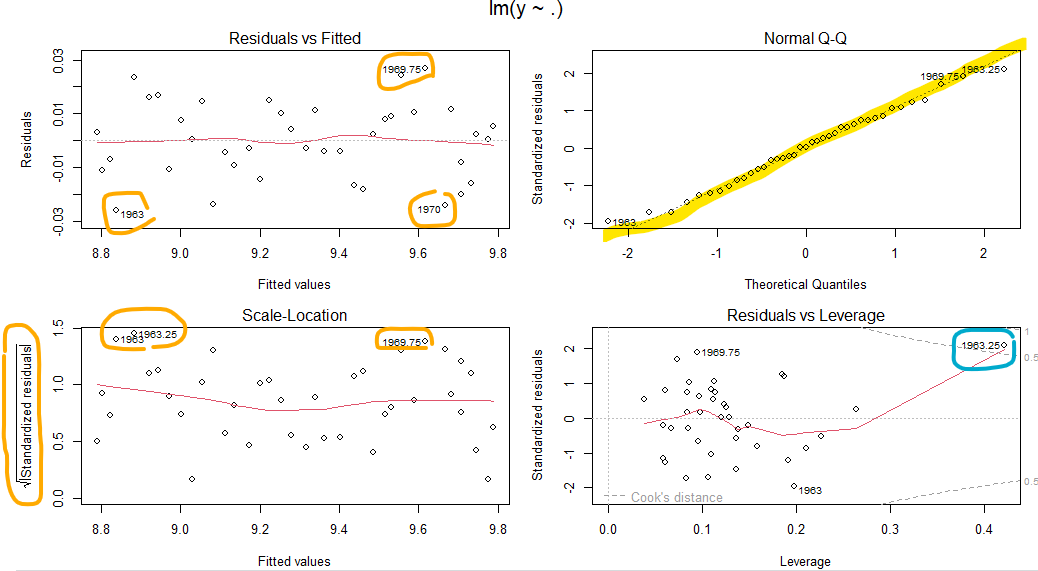
さて、上記の重回帰分析の結果を吟味するのに
回帰診断図 (diagnostic plots)
というものを描くのだそうな。
左上から、当てはめ値(fitted values)に対する残差のグラフ。オレンジで囲みましたが、数字が書いてある奴らはハズレ方が多きいので、個別に吟味せよ、ということらしいデス。知らんけど。
右上は、QQプロット(quantile-quantile)というものだそうな。バラツキの分布が正規分布に近ければ直線になるらしいデス。知らんけど。
左下は、sqrt(残差の絶対値) の Scale-Location プロットだそうです。SLプロットと呼ばれれるらしいっす。なんで平方根とるのかというと、「歪みを減らすため」だそうです。背景分かっておらん素人には分からんな。まあ、残差の絶対値の平方根とっているので、上の方にいる奴らがヤバい奴らだと。
最後右下は、Cook の距離のプロットというものらしいです。右の方に点線で0.5とか書かれているけれども、点線より外側が0.5を超えて(距離が遠い)ということみたいっす。そこで青で囲った点が大きく外れたヤバイ奴だと。
ううむ、よくわからんなあ。いつものことだけれども。