
今回からホントに定積分です。上端、下端が数値で指定された定積分ならば、結果も数値になるのであろう、さすれば結果も一発でバッチリ得られるであろう、などと甘くみてました。たしかに数値で結果が得られるのですが、「数学の宿題」的にはなんだかな~。やっぱり後の整理が辛いというかメンドイです。
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の教科書(参考書、問題集?)の例題をMaximaの練習に使わせていただいております。
大昔、大学生のときにこういう御本が欲しかったです。
※以下のMaxima/wxMaximaバージョンで実習させていただいております。
-
- Maxima 5.46.0
- wxMaxima 22.04.0
最初の例題、パッと見の数値に騙されました。
定積分の最初の練習が以下に。前回同様、
-
- まず積分記号の形のままで眺め
- その「名詞形」をev(%, nouns)で評価して積分結果を得る
というスタイルです。前回の不定積分と異なるのは、integrate()の第3引数として下端、第4引数として上端を指定している点。こんな感じ。
evした結果は%o2のように、なんだかな~な形なのですが、radcanに渡せば整理してくれました。しかし、黄色のマーカ部分をご覧ください。私は最初、
72の2分の5乗
と読んでしまい。混乱しました、忘却力の行き着くところ、とうとう分数指数の計算もできなくなったかと。教科書の例題なので分子は「28掛けるルート2」になるハズと知っておる故の混乱です。上のような解釈では一致しませぬ。
しばらく混乱した挙句、上記のマーカ部分は72ではなく、7と2の間にスペースが、つまりはMaxima上は掛け算が挟まっていることに気づきました。「7掛ける2の2分の5乗」です。以下検算。
ううむ、人騒がせな。数字と数字の間に挟まったスペースの掛け算。たしかに72と続けて書くよりスペースが広い。でも、やめとくれでないかい。
例題その2、根号の有理化、今後の課題?
次の問題が以下に。定積分の評価一発でお答えがでましたが、「数学の宿題」的にはなんだかな~。大昔「有理化せよ」としつこくならった記憶がよみがえります。年寄は昔のことは覚えているのよ。
上記マーカ部分をの分子、分母を取り出してそれぞれルート3を乗ずれば以下のような感じ。しかし、その後で分子を分母で割ると「余計なもの」は約分されてしまうっと。
どうも、Maxima様の設定を上記のようなデフォルトから変え、処理の方法を変更すれば「有理化」した表現することができないこともないみたいっす。でも今回は面倒なのでパス。「有理化」しなくてもいいじゃん、計算できるし。。。
例題その3
こういう感じを求めていました。定積分一発、お楽。
例題その4、logの引き算を割り算に直すのが依然課題
次の例題の解にはlogが含まれとります。黄色のマーカ部分、log(4)は2log(2)とできるので2をくくりだしたあとのlogの引き算をlogの中の割り算に変換したいです。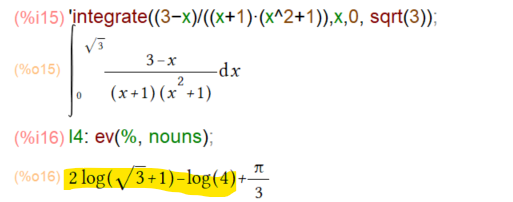
式の中の所望の項を取り出すのはできるようになったのですが、肝心の引き算を割り算に変形する方法がいまだしであります(割り算を引き算にするのはradcanでできます。)
結局、下の黄色のマーカ部分が「数学の宿題」的な解答になるのでありますが。
まあ、メンドイけど、積分そのものはできているので、後はコマケー話だぜ。それでよいのか?




