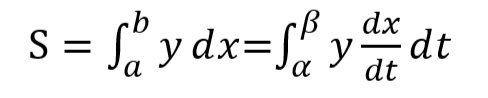前回は陰関数、今回は媒介変数です。ハート型です。バレンタインだからというわけでないです。メンドい感じのグラフだな、これは。これも修行と。違うか。今回の媒介変数の例題では、プロットだけでなく積分も媒介変数のまま行うことになるみたい。要は置換積分なんだけれども。高校生なら覚えている置換積分も、年寄は忘却の彼方。どうする?
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の教科書(参考書、問題集?)の例題をMaximaの練習に使わせていただいております。
遥かなるかな太古の時代、大学生のときにこういう御本が欲しかったデス。
※以下のMaxima/wxMaximaバージョンで実習させていただいております。
-
- Maxima 5.46.0
- wxMaxima 22.04.0
媒介変数表示された関数のプロット
媒介変数使ったプロットは遥か忘却の彼方の第27回でもやっています。このときの方がムツカシー奴をやっつけていたような。ともかくparametricというキーワードをつければ簡単。今回は以下のとおりでプロットできます。
wxplot2d([parametric, sin(2*t), sin(3*t),[t, 0, %pi]]);
さて例題のグラフが以下に、媒介変数表示なので、X軸はsin(2t)だし、Y軸はsin(3t)っす。プロットは書けたけれど、定積分はどうしたらよかですか?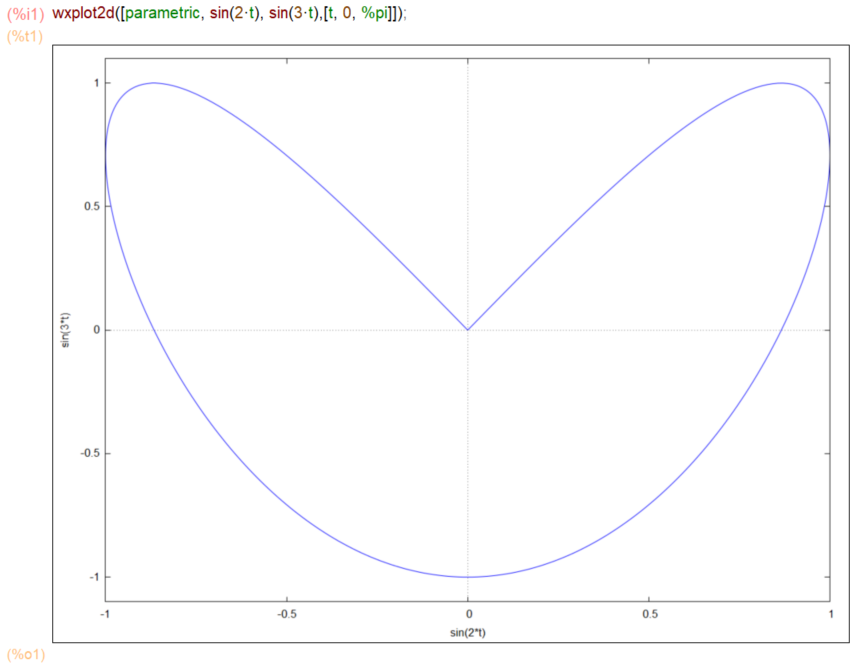
xで積分からtで積分へ「置換」
例題のXとYは以下のようでした。どちらも媒介変数 t によって記述されております。
まあ、最初からY=tの式に変形しようなどとは思いませぬ(最初、Y=Xみたいな形でそのまま媒介変数表示のまま積分できないかとやってみましたがうまくいきませなんだ。お馬鹿な私。)自分じゃ解けそうにもないし。結局、高校で出てくる置換積分の公式に立ち戻って解くことにいたしました。以下です。
積分区間は xで書くと-1から1まで、tで書くと-π/2からπ/2であろうと。いい加減じゃな。さらにグラフを見て考えるに、Y軸対称。-π/2から0の面積と0からπ/2の面積は等しい筈。結局、0からπ/2までの区間で積分すればよろしかろう、と。ホントか?
まずは置換積分のため、dx/dtの部分を計算。あら、ここは微分しないとならないのね。簡単な微分ですがMaxima様にお願いしてます。こんな感じ。
置換積分の公式に上記をぶち込むとH(半分の面積なのでHとしてみました)の定積分は以下に。
Hの積分はMaxima様にお願いすれば、一撃で求まります。そして「半分」なので忘れずに2倍すれば面積になると。なんだか意外と簡単に求まってしまったデス。置換積分、恐るべし。何をいまさら。