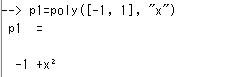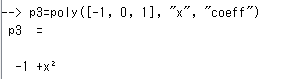Scilabの基礎もないところに泥縄式でいろいろやってみているので、毎度「よくわからんな」が続出。砂上の楼閣状態です。伝達関数を記述するときに「お世話になる」polyという関数もそう。z=poly(0, “z”)みたいな「おまじない」を唱えること度々。どうも多項式を定義するためのものらしいんだけども。。。
※「手習ひデジタル信号処理」投稿順 Indexはこちら
※動作確認に使用させていただいているのは、Scilab 6.1.1(Windows版)です。
多項式、多項式を定義する際に使用される変数
冒頭のアイキャッチ画像にも掲げましたが、伝達関数などを定義するときにx=poly(0, “x”)みたいなおまじないを書いてから記述することが多いと思います。
この「おまじない」を省くとどうなるかというと、こんな感じ。怒られてしまいました。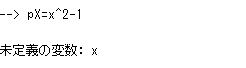
変数ブラウザをみると、この「おまじない」の効果が明らかです。
xという「多項式」変数が定義されており、その変数を使ってpXが記述されているのだ、と。
ちなみに「おまじない」無しに、多項式の記述に使える変数が事前定義されています。以下の2つ。
-
- %s
- %z
%をつけなければならない点、入力がちょいとめんどうになりますが。こんな感じ。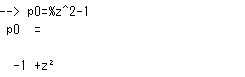
変数名の入力が多いときは「おまじない」方式の方がよさそう。しかし x=poly(0, “x”)の0って何よ?
poly()の定義の仕方の3種類
いつもお世話になっておりますScilab Online Help(日本語)の以下のページを参照してみます(日本語といいつつ、このページはほぼほぼ英語。)
poly()の第1引数のデフォルトは、rootsでした、「根」ね。第2引数はシンボルの文字列であると。つまり x=poly(0, “x”)というものはシンボルxで書かれた根0を持つ多項式を変数xにするということみたいです。知らんけど。
ということは何かい、根を列挙したら多項式を作ってくれるのね。こんな感じ。
X^2 – 1 = 0 の根は1と-1。中学生の数学ですが、便利ね。実は第3の引数あり上記のような記述はデフォルト値を使った省略形でした。「第一引数が根」の場合は以下のように書くのが省略なしみたいっす。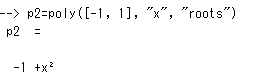
“coeff”とすると、多項式の係数のリストから生成できるのでありました。なお、「昇べきの順」がデフォルトみたいっす。
さらに、以下のように第1引数に正方行列を与えると、「固有方程式」(Eigen Equation)を作ってくれるみたいです。中学卒業高校数学?
上記の行列Aは、別シリーズ「忘却の微分方程式(48) 反復練習12、固有値と固有ベクトル、対角化 Maxima」で使用させていただいた例題です。その時もとめた(計算したのはMaxima様ですが)固有方程式は固有値λ1、λ2を用いて以下のようでした。
(λ1-3)^(1)*(λ2-2)^(1)=0
目障りな^(1)は、固有値の多重度が1というところからきてます。λをxにしてしまって、Maxima様に式を変形していただくと以下のようです。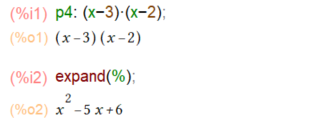
昇順、降順の違いはあれ、Scilabの計算結果とMaximaの計算結果が一致。まずはめでたい。
roots()、horner(), coeff()
poly()の扱いに少し慣れたので、poly()関係の関数をいくつか見ていきます。まずはroots()、その名の通り根を求めるもの。上記のp4を渡してみるとこんな感じ。
根は当然のように複素数範囲で求めてくれちゃうのね。でもま虚部は0だし元の固有方程式の根に戻ったと。
つづいてhornerです。こちらは多項式の変数になにか数値を代入したときの値を求めてくれるみたい。スカラーだけでなく、行列突っ込んでも大丈夫とな。流石だ。
さて、以前の回で「同名の変数を定義して痛い目にあった」coeffです。
coeffに多項式を渡すと係数ベクトルを返してくれます。やはりデフォルトは昇べき順。しかし、降べきの順でも特定次数だけでも扱ってくれるのでありました。こんな感じ。
第2引数にとりだす次数をベクトルで与えればよいみたいです。
なんとかpolyは分かった、ホントか?次はpolyを使っていろいろ?