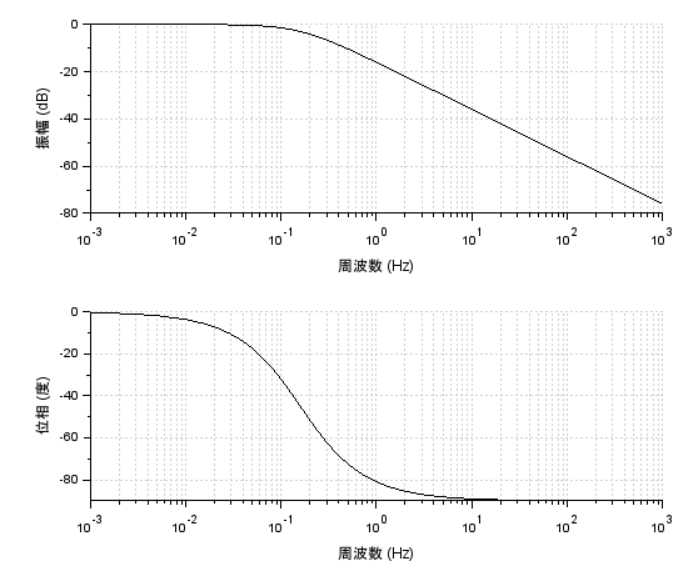
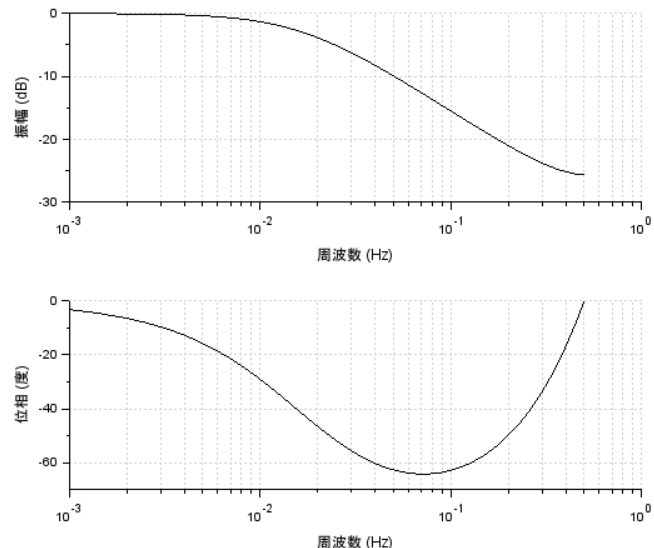
前回 poly を使った多項式の定義がわかったような気がしたので、今回はそれを使って伝達関数を定義してみます。これまた過去に毎度もお世話になっている割にはなんだか謎なsyslinという関数を使って「使える形」にしていきます。線形システム?いや伝達関数のまま?なんじゃそりゃ。調べてみれば違いは一文字?
※「手習ひデジタル信号処理」投稿順 Indexはこちら
※動作確認に使用させていただいているのは、Scilab 6.1.1(Windows版)です。
多項式が記述できれば、伝達関数も書ける?
多項式が記述できれば、伝達関数は分母/分子が多項式の有理式として表現できるのだからそれでよろし、と思いきや、表にはでてこない大きな一歩を踏み出さないと「使える伝達関数」にはなってくれないようです。
以下ではpolyをつかって文字 ‘s’ を多項式を表記するためのシンボル(多項式)として、伝達関数Hsをsを使って記述。そしてその先の一歩、syslin()関数を使って ‘c’ 、つまり連続な「ドメイン」の線形システムとしておるのです。
上記のようにsLとHsの見た目は一緒の伝達関数っす。でもね、bode関数でボード線図を描いてもらうとその違いは明らかです。sLの方はほれこのように。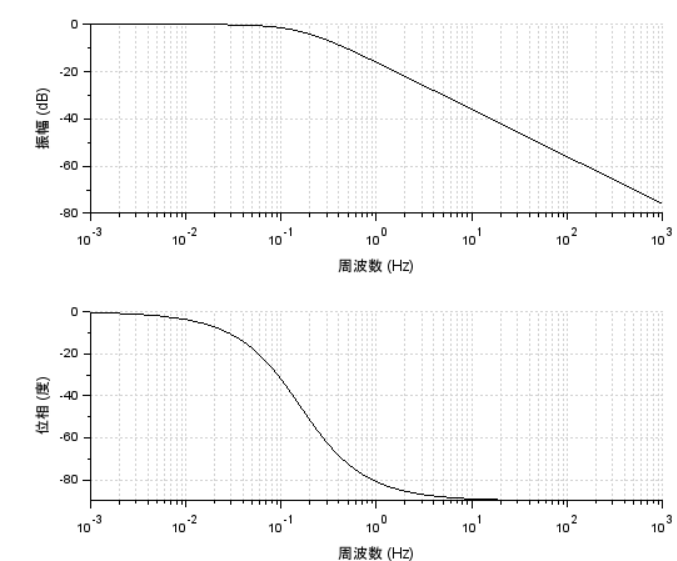
ところがHsの方は、あえなく撃沈。「時間領域が未定義」らしいです。
以下は、いつもお世話になっておりますScilab 日本語Helpのsyslinのページへのリンクです。
上記を読んでSilab素人は、syslinにかけると行列A、B、C、Dで表される「線形システム」に変換されて記憶されているものと勝手に思い込んでました。「線形システム」について素人は多くを語りますまい。以下のサイトなどどうぞ。
しかし、今回調べてちょいと愕然としたのは、syslinに引数あたえるフォーマットも複数あり、確かに、A、B、C、Dで与える方法ならばそのようですが、伝達関数を与える方法の場合、伝達関数の分母、分子をわけて記憶しているだけみたいです。違いはたったの「一文字」です。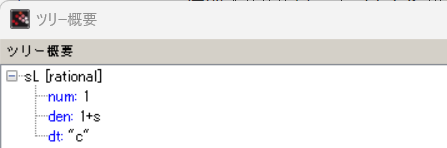
上のdtのところに”c”と書かれておりますな。これは連続領域でのsyslinということでわけもわからず第一引数に与えたものにほかなりません。一方、元のHsはというと
分子num, 分母denは一緒ですが、dtが無し。つまりは「計算できる」伝達関数であるためにはdtの定義が重要みたいです。知らんけど。
離散ドメイン、サンプリング時間指定の場合
syslinがやっていることがおぼろげながら分かってきたので、こんどはzで記述できる離散ドメインの場合をやってみます。テキトーに伝達関数を書きました。zと書くか、sと書くかは単に人間のわかりやすさのみ。本質は ’d’ 離散ドメイン指定だと。
実際にzLの中身を覗いてみるとこんな感じ。dtは”d”だと。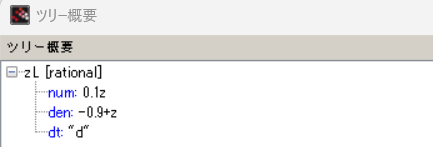
そしてdtが”d”だと bode()関数に渡したときの挙動は異なります。
問題はx軸です。ただ離散ドメインだと宣言しただけでは具体的なサンプリング周波数などは分からないのです。離散的な周波数応答はサンプル時間Tが決まらないと具体的に計算できないので、「正規化周波数」で計算しておると。そういうことだったのね。
実は syslinに与えるのは、’d’ のサンプル時間が未決定の抽象的な離散ドメインでなく、具体的なサンプル時間を与えてしまってもよいのでした。こんな感じ。
見た目の伝達関数は同じですが、周波数応答のx軸(周波数)には具体的な周波数が入ってきました。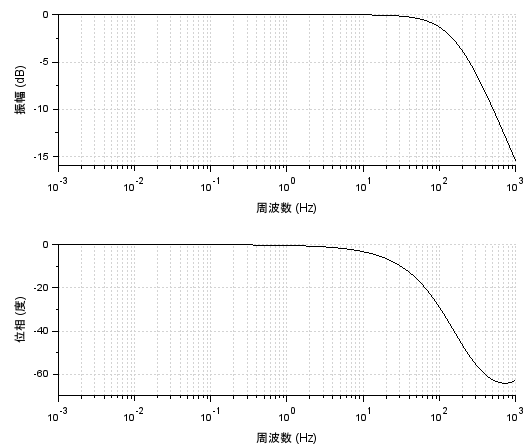
そういうことだったのか。
tf2ss、伝達関数から線形システム表示への変換
上記のように伝達関数形式でsyslinしても中身は伝達関数のままみたいです。しかし、tf2ssという関数があり、これを通すことで行列A、B、C、Dで表される「線形システム」に変換できるみたいっす。まずは連続ドメインの場合。
続いて離散ドメインの場合
連続から離散ドメインへ変換
そして以下に日本語Helpのある、dscrという関数を使うと連続ドメインで定義した伝達関数をサンプリング時間を指定した離散表現に変換できるみたいです。
最初連続ドメインで考えていても、DSP実装となると離散へ行かないとならないので必須か?ホントか?
上記だと、ABCDの線形システム形式でピンとこないので、古めかしい伝達関数形式にすることもできます。今度はss2tf関数とな。
おお、これが知りたかったんだ。計算できる?