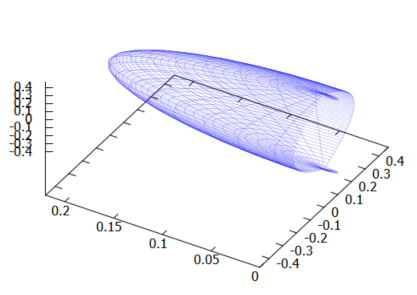
前回は、ある軸にそった断面積が分かるときに体積を求める例題でした。今回はその応用という感じ?曲線をある軸の周りに回転させたときにできる曲面と「回転軸座標のある範囲」で囲まれる体積を求めよ、という感じっす。そのままでは前回とあまり変わらないので、ちょいとひねり、いや回転を加えてるみたい。
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の教科書(参考書、問題集?)の例題をMaximaの練習に使わせていただいております。
遥かなるかな太古の時代、大学生のときにこういう御本が欲しかったデス。
※以下のMaxima/wxMaximaバージョンで実習させていただいております。
-
- Maxima 5.46.0
- wxMaxima 22.04.0
今回の例題
今回の例題は、以下の%o2の曲線(xからみたら2次関数なので放物線ですわ)とy=0で囲まれた部分をx軸、およびy軸を回転軸にそれぞれ回転させたときできる体積を求め、x軸回転の体積とy軸回転の体積が一致するときの a の値を求めよ、という問題であります。文字で書くとしんどいな。冒頭のアイキャッチ画像にY軸回転のときの曲面の図を掲げました。蛇足ですが、回転体の3D表示、メンドイというより年寄の頭の中で軸がグルグルして分けわかりません。これはこれで練習してみないとダメな感じがします。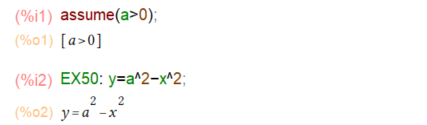
さて、y=f(x)なる曲線とX=aとX=bで囲まれる面をX軸回転させたときの体積は以下です。断面積を Syは πy2 になるので、前回の延長ですな。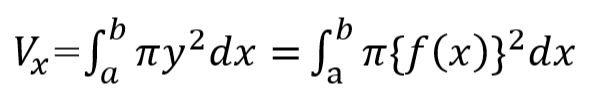
当然Y軸回転の断面積 Sxはπx2 であらわせます。今回例題で断面積の式を計算しておくとこんな感じ。
上記で断面積の式は分かりました。積分範囲を決めるために、X軸回転ならばX軸との交点、Y軸ならばY軸との交点を求めておかねばなりません。こんな感じ。solve先生、大活躍。
X軸回転の体積を定積分。integrate関数でで定積分など一撃ね。
上記でX軸回転とY軸回転の体積が求まったです。問題としては、これが等しくなるときのaを求めよ、ということです。最後にsolve様に再びお願いVX-VY=0となるような a は何?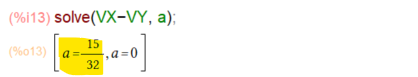
黄色いマーカの方がお答えです。assume(a>0)しているのだけれども、こういうときには事前にはじいてくれたりしないのね。このくらいは老人にも分かるからいいけど。
まあ、ともかくお答えが求まり良かった。しかし、回転体の体積のグラフ化もうちっとカッコよくやりたいもんです。また、次回か。