前回mut無でmandelbrot集合を描けたのでフラクタルづきました。こんどはお馴染みシェルピンスキーのギャスケットだと。しかしその前にPascalの三角形だろ~。mCn(コンビネーション; 組み合わせ)が3角形にならぶ中学生の問題。2nのPascalの三角形を偶奇で塗り分けるとシェルピンスキーと。ホントか?
※『RustにいればRustに従え』関係記事 index はこちら
※動作確認は、Windows11のWSL2上にインストールしたUbuntu20.04LTS上のrustc 1.64.0 (a55dd71d5 2022-09-19) で行っています。
Pascalの三角形
遥かな昔、中学生のときに、順列、組み合わせの授業のときに、先生がPascalの3角形を黒板に書いたような記憶があります。忘却力の年寄ですが、昔のことは覚えているのであります。ただし、間違って記憶していることも多いケド。
頂点に0C0(=1)をいただき、その下の行は、1C0、1C1、そのまた下は、2C0、2C1、2C2と末広がりに続く数字の山であります。
無限に続くこの数字の列を偶奇で塗り分ければ、典型的なフラクタル図形、シェルピンスキーのギャスケットが現れるのだそうな。ま、今回はPascalの三角形を出力しておしまいだけれども。
Rust版Pascalの三角形
例によってアカラサマな mut (この変数は書き換えるよ~んという指定)無、for文使った繰り返しは最小(Rustのforはシンタックス・シュガーらしいのでそれほどこだわる必要ないのかもしれないです)で計算してみたものが以下に。
main()関数の中で20とキメウチで20段まで出力するようにしたソースが以下に。
fn sub(n_len: usize, arg: Vec<i32>) ->Vec<i32> {
(0..n_len).map(|i: usize|
if i == 0 {
1
} else if i == (n_len - 1) {
1
} else {
arg.get(i-1).unwrap() + arg.get(i).unwrap()
}
).collect()
}
fn sub2(n_max: usize, n_len: usize, arg: Vec<i32>) {
for xa in arg.clone() {
print!("{} ",xa);
}
println!();
if n_len >= n_max {
return;
}
let nexta:Vec<i32> = sub(n_len, arg);
sub2(n_max, n_len+1, nexta);
return;
}
fn main() {
println!("1");
let test = vec![1i32, 1];
sub2(20, 3, test);
}
なお、上記を見ればお分かりのとおり、まともに「コンビネーション組み合わせ」を計算するのは憚られたので、上の段の数字をのぞき見して下の段の数字を作る方法で計算してます。簡単だし。
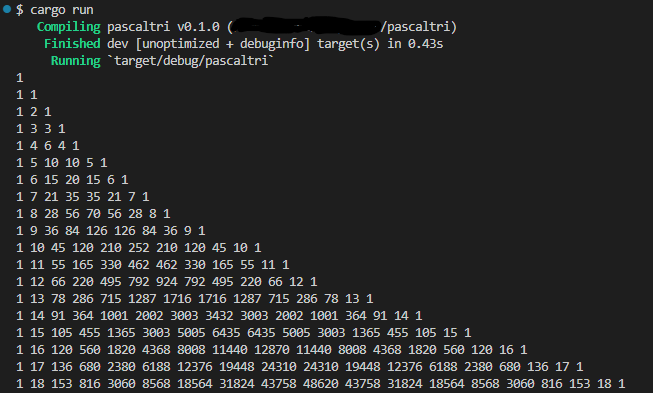
実機実行結果
左詰めなので綺麗な三角形ではないけれど、多分Pascalの三角形(上の5段目までしか確かめてないです。メンドイ。)
次回はシェルピンスキー?