前回、前々回とPascalが続きました。Pascalにm2を掛ければNewtonという親父ギャク?をものにすべく、今回はNewton法です。アカラサマなmut無、for無で書けました。古くから研究されつくした算法なのでいろいろ注意点がある筈ですが、全部踏みつぶしてしまったヤッツケなコードです。4則演算のみで√2だと。
※『RustにいればRustに従え』関係記事 index はこちら
※動作確認は、Windows11のWSL2上にインストールしたUbuntu20.04LTS上のrustc 1.64.0 (a55dd71d5 2022-09-19) で行っています。
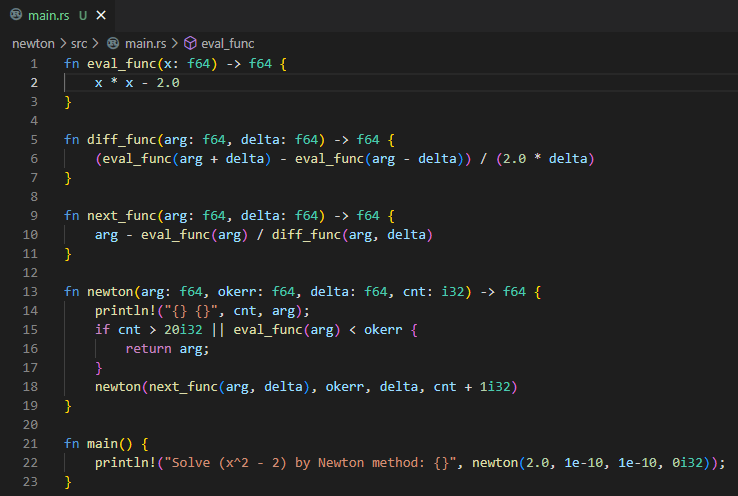
手抜きのNewton法のソース
以下は配慮の足らないNewton法のやっつけコードです。一番上の eval_funcという関数内で
x * x – 2.0
と書かれているのが、解くべき方程式の左辺(右辺は0)です。2次方程式なら解の公式でも解けますが、ここの部分をテキトーに別な式に書き換え、末尾の以下の呼び出し初期値を適切に変更すれば、他の方程式の根も求めることは可能(根が存在すれば)な筈。
newton(2.0, 1e-10, 1e-10, 0i32))
まあ、実用的には立派なライブラリがいろいろある筈なので使うことは無いでしょうが。
fn eval_func(x: f64) -> f64 {
x * x - 2.0
}
fn diff_func(arg: f64, delta: f64) -> f64 {
(eval_func(arg + delta) - eval_func(arg - delta)) / (2.0 * delta)
}
fn next_func(arg: f64, delta: f64) -> f64 {
arg - eval_func(arg) / diff_func(arg, delta)
}
fn newton(arg: f64, okerr: f64, delta: f64, cnt: i32) -> f64 {
println!("{} {}", cnt, arg);
if cnt > 20i32 || eval_func(arg) < okerr {
return arg;
}
newton(next_func(arg, delta), okerr, delta, cnt + 1i32)
}
fn main() {
println!("Solve (x^2 - 2) by Newton method: {}", newton(2.0, 1e-10, 1e-10, 0i32));
}
今回、上記の設定では、ルート2を求めることにあいなります。f64型のsqrtメソッドに頼ることなく、4則演算だけで無理数(の近似値)がもとまります。流石ニュートンは偉大。テキトーなところで打ち切っているのでありますが、上記は素性がいい方程式なので収束早、とってもはや。
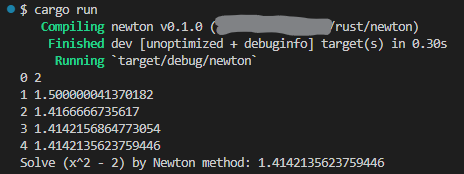
実行結果
実機、実行結果が以下に。1.41421356(ひとよひとよにひとみごろ)までは覚えております。ここまでOK。後の桁は知らんけど。
繰り返し的にはたった5回の計算でここまで到達。まあ素性のいい式だからな。行ったり来たりする根性悪な式も試せよ。