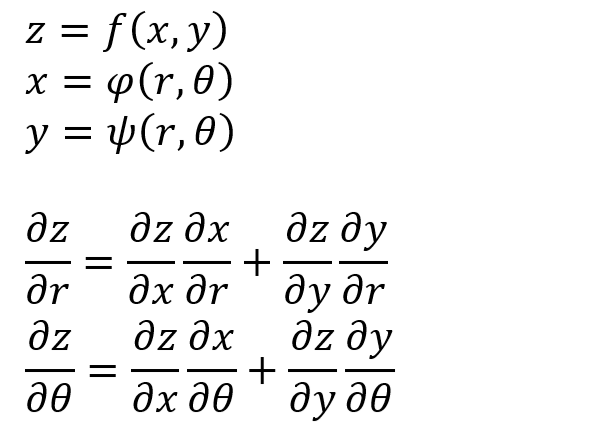前回につづき今回も合成関数の偏導関数です。今回の方が合成前の関数の偏導関数をわらわらと求めて、最終的に合成関数の偏導関数を求めるという点では「ありがち」な感じです(個人の感想デス。)まずは教科書の定理(公式?)に沿って解いてみましたが手数多くてメンドイです。素のままMaxima様にお願いした方がやっぱりお楽。
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の教科書(参考書、問題集?)の例題をMaximaの練習に使わせていただいております。
遥かなるかな太古の時代、大学生のときにこういう御本が欲しかったデス。
※以下のMaxima/wxMaximaバージョンで実習させていただいております。
-
- Maxima 5.46.0
- wxMaxima 22.04.0
今回練習する例題
以下のときに ∂z/∂r、∂z/∂θ を求めよというのが問題です。淡々とそのまま入力すれば「何も考えず」にMaxima様が解いてくれるのは前回で分かってます。それではあんまりなので、最初は注意して冒頭のアイキャッチ画像に掲げた定理(公式?)を使うようにしたいと思います。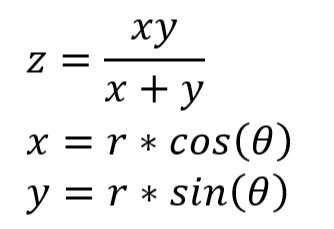
定理(公式?)通りの解法
最初に、∂z/∂x、∂z/∂y を求めておきます(この順番何気に問題回避してます。)
予想どおり、ただdiff(z,x)などとしただけではメンドイ式がボロリンと出てきて非常に見ずらいので、ratsimp()で整理して、factor()で因数分解して「整形」した後の結果にしてます。多少は学んでいる?まあ、別々に偏微分しなくても元が対称だから片方計算すれば分かるのだけれども。
続いて上記の∂z/∂x相当のdzxと∂z/∂y相当のdzyをx,yでなく極座標で書き直してます。今度は三角関数なのですが、ここは三角関数用ではなくフツーのratsimp+factorで再び整理。
ここまで来てから、ようやくx, y を定義し、∂x/∂r、∂x/∂θなどを計算できるようにいたしました。そこでおもむろに定理(公式?)を適用。
上記で一応、解にたどり着きはしました。でもちょっと見ずらいので、最後にいたって三角関数用の整理を行ってみます。こんな感じ。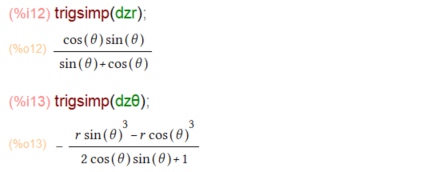
こんなもんかい。
TIPS
上記のようにX、Yを極座標定義してしまった後で、再びzをxで微分しようなどと試みると怒られました。エラーメッセージが以下に。
第2の方法、Maxima様にお任せ
第2というほどの方法ではありませぬ。Maxima様に丸投げっす。x, yを極座標で定義したあと、zをx, y で定義すれば、何も言わずに極座標。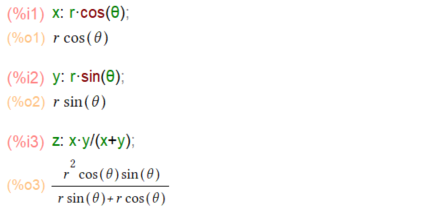
そして上記のz を r で微分すれば∂z/∂r、 θで微分すれば∂z/∂θが求まると。微分したままであると三角関数の式が大層なので、trigsimp()一発。
どうみても、Maxima様にお任せする方が簡単だし。