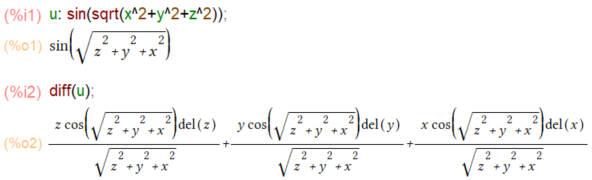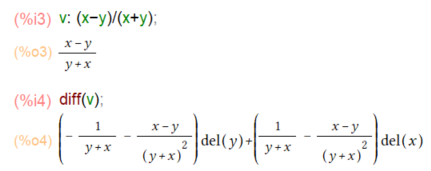前回も偏導関数でした。偏微分の先には全微分あり?で、今回は全微分です。なんのこっちゃ?Maxima様にお願いする分には、全微分も「いつもの」diff()関数一発で求まります、一撃。ただし「全部(変数について)微分しろ」という指定なので事前の取り決め必須。人間のように「多分これは定数ね」とか勝手に判断してくれません。
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の教科書(参考書、問題集?)の例題をMaximaの練習に使わせていただいております。
遥かなるかな太古の時代、大学生のときにこういう御本が欲しかったデス。
※以下のMaxima/wxMaximaバージョンで実習させていただいております。
-
- Maxima 5.46.0
- wxMaxima 22.04.0
全微分
数学素人が全微分を説明する「図」を描こうなどとは思いませぬ。どこかに適当なものがないかと思って調べたらKIT様の以下のページが良さげでした。あざ~す。
図をみりゃ分かった気になる?のでした。
さて、微分関係をなんでも引き受けてくださるMaxima様の diff() 関数ですが、全微分も例外ではありません。同じdiff()関数一発で全微分も求まります。「全」微分をどう指定するのと問えば、「微分する変数を指定しない」ければよいと。逆説的な?
いつもお世話になっておりますMaximaの日本語マニュアルページが以下に。
ただし「指定しない」ことで注意しなければならない問題もあり。後でそういう例が出てきます。
素直に解ける課題
まずは素直に一撃で解ける課題を練習してみます。最初がこちら。
diff(u)のところを du のように読み替え、del(z) などを dz などのように読み替えると数学の教科書的な表記になるかと思います。それにしても del(z)とかイマイチ直観が働かない書き方デス。慣れろよ、自分。
diff()一発でとけるのはお楽でよいな。
何が変数で何が定数なんだか
続いて、事前準備のいる問題です。以下の緑のマーカ部分が全微分するべき式でありますな。そして数学の教科書としては、a>0、a!=1 などと条件がかかれており、これで、aは定数、x, y, z が変数だと分かります(多分、ヒト?AI?は。)
でもMaxima様におかれましては、黄色のマーカ部分、a は定数だよ、を除くと、aも変数だと思って無理やり微分しようとするみたいっす。知らんけど。ちょっと期待と違う結果が出てくるので delare(a, constant) を忘れずに宣言しておくこと必須です。
上記のように事前の定義がしてあれば、なんのことはない、全微分そのものは一発です。数学頭が鈍いとついついこういうところを見逃すよなあ。忘却力だし、しかたない。。。