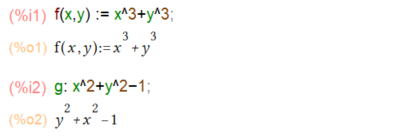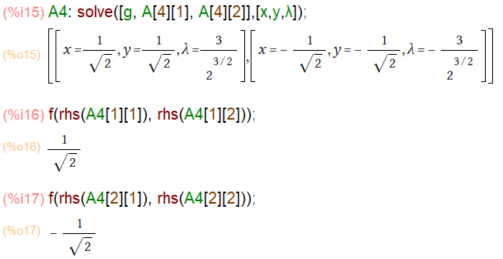数学不得意の私メはラグランジュ大先生のお名前を聞くだけで恐れ入って逃げたくなりますです。しかし、今回は名高い「ラグランジュの未定乗数法」です。条件付き極値問題とな。まあ実際の計算はMaximaにお任せなので淡々と「未定乗数法」すれば良い、といいつつやっぱりメンドイ。しつこく陰関数も登場。
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の教科書(参考書、問題集?)の例題をMaximaの練習に使わせていただいております。
遥かなるかな太古の時代、大学生のときにこういう御本が欲しかったデス。
※以下のMaxima/wxMaximaバージョンで実習させていただいております。
-
- Maxima 5.46.0
- wxMaxima 22.04.0
今回の問題
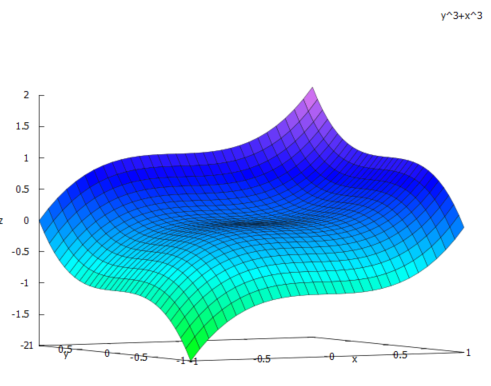
今回は「条件x2+y2=1のもとでx3+y3の極値を求めよ」という問題です。雰囲気をみるために、x3+y3 の3次元プロットを描いてみたです。コマンドが以下に。
plot3d(f(x,y),[x,-1, 1],[y,-1,1]);
上記xy平面上、上のプロット範囲にちょうど接するような円周を描いてそのときの最大、最小を求めるのだと。分かっちゃいるけど「素では」解けません。
ラグランジュの未定乗数法
さて肝心の「ラグランジュの未定乗数法」ですが、参照させていただいている教科書には解説が書かれておりますがネタバレはマズいし、数学素人が解説するのは憚られるし(恐れ多いラグランジュ先生だし)、で以下のURLなどご覧くだされ。いつもお世話になっております「高校数学の美しい物語」様の解説ページです。
今時の高校生は「ラグランジュの未定乗数法」でビシバシ問題解いているのですかね。
Maximaにて解く(解いていただく)
さて、Maxima様にお願いするためには、問題を入力せねばなりませぬ。極値を求める関数をf(x, y)とおいて、条件を g とすると以下のように書けますかな。
さて、「ラグランジュの未定乗数法」を適用するために、ラグランジュの乗数 λ を導入して F を立てまする。そしてFをxとyの両方で偏微分。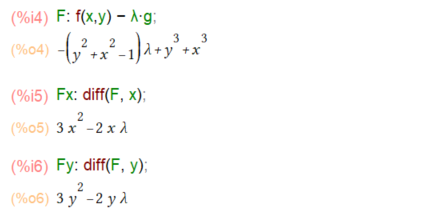
上記で求まった FxとFyについて Fx=0、Fy=0となる x, y の組を求めれば、これらが極値を与える点(x,y)の「候補」となるみたいっす。algsys()関数は良いです。自分じゃ絶対解ける気がしないっす。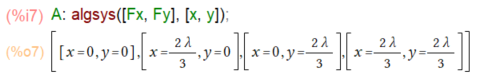
上記のように、4点の候補が見つかりました。まだラグランジュ乗数のλが入ったままだけれど。
上記4点の候補のうち、最初と2番目の候補を条件gに当てはめ、λを決定してみます。
上をみると最初の候補x=0, y=0は解なし。gはx2+y2=1なのであたりまえだけれど。第2の候補は(1, 0)で1、(-1,0)で-1という極値候補を持つことが分かりました。それにしてもsolveでλを求めたけれども、求めたときにはもう不要と。ラグランジュ乗数の威力というか儚さというか。
さて3番目の候補で計算、といってsolve関数にみなお任せです。)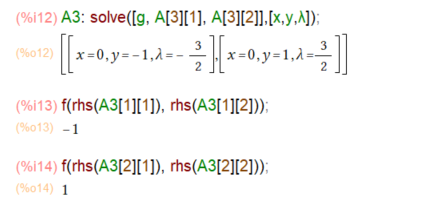
こんどは(0, -1)で-1、(0,1)で1とな。
最後のやつは 1/√2は明らかに1より小さく、-1/√2は-1より大きいので候補から除外ね。すると、
-
- 最大値は、(1, 0)で1、(0,1)でも1
- 最小値は、(-1,0)で-1、(0, -1)でも-1
なんとか求まったけれども、メンドイっす。文句を言うなよ、自分。