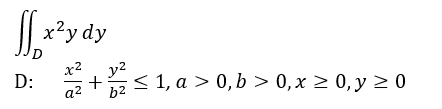前回はドーナツ型の積分領域を極座標変換して２重積分しました。今回も極座標変換ですが、積分領域が楕円になりました。前回同様、再びヤコビアンさんが登場しますが、円の時とはチョイと違うみたいです。変数変換にも楕円の長軸、短軸長さが入ってくるし。まあ、極座標変換してしまった後はMaxima様の一撃にてお答えは求まるっと。
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の教科書（参考書、問題集？）の例題をMaximaの練習に使わせていただいております。
遥かなるかな太古の時代、大学生のときにこういう御本が欲しかったデス。
※以下のMaxima/wxMaximaバージョンで実習させていただいております。
-
- Maxima 5.46.0
- wxMaxima 22.04.0
積分領域Ｄが楕円のときの極座標変数変換
以下のような場合、前回の円のときのフォーミュラにちょいと手を加えて以下のように書けると。いや、前回の円が以下の特殊な例、a=b=1だったというべきか。数学不得意の老人にはサッパリです。
変数変換のところと、再び登場のヤコビアンＪのところに黄色のマーカを引いておきましたです。これさえ覚えていれば楽勝。ホントか？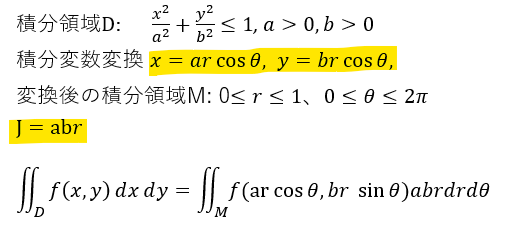
今回の例題
まずｘ、ｙ座標の領域Ｄで記述された今回の例題が以下です。
積分領域Ｄは、「楕円の一部」みたいです。前回 draw2dを使って陰関数の不等式を含む領域を塗りつぶす技を取得（？）したので、喜んで上記のＤに適用してみます。ただし、a、ｂと文字定数のままではグラフに描けないので「仮にa=3、b=1」としてグラフ化してみます。
コマンドが以下に。
draw2d(x_voxel=100, y_voxel=100, grid=true, proportional_axes = xy, region(x^2/3^2+y^2/1^2<=1 and x>=0 and y>=0, x, -0.5, 3.5, y, -0.5, 1.5))
領域Ｄのプロットが以下に。楕円の４分の１を切り出した形なのね。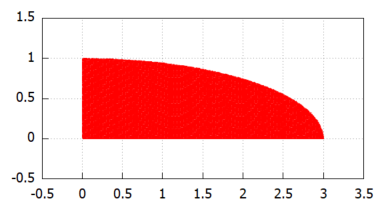
これで変数変換後の積分領域Ｍも一目瞭然であります。例題式を変数変換して書き直すと以下のようです（忘れずにヤコビアンさんも乗じますです。）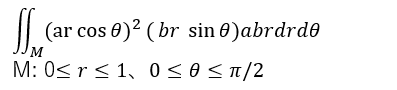
ここまでくれば後はMaxima様にお願いすれば一撃。
お答えが求まりました。それにしても不等式を組み合わせた領域を塗りつぶせるの便利。