前回までは2重積分で変数変換を練習してきましたが、今回は3重積分での変数変換です。積分領域を確かめ、ヤコビアンさんを計算して、積分変数を変換した積分を行うという手順は2重積分のときと変わりませぬ。しかし、変数が増えるとぐっとメンドくなるのよ。でもMaxima様にお願いする分には2個も3個も関係ね~と。
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の教科書(参考書、問題集?)の例題をMaximaの練習に使わせていただいております。
遥かなるかな太古の時代、大学生のときにこういう御本が欲しかったデス。
※以下のMaxima/wxMaximaバージョンで実習させていただいております。
-
- Maxima 5.46.0
- wxMaxima 22.04.0
今回の例題
別ソフトにて清書したものを以下に掲げます。積分領域もアリガチならば積分も素直な感じで嬉しいです。ま、解くのはMaxima様なんだけれども。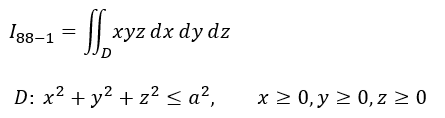
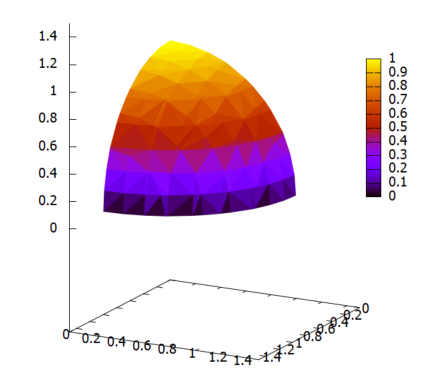
積分領域Dをグラフに
定数 a のままではグラフに描けないので、一例ということで a=1 と一番簡単な形でグラフを描きます。また、体積を塗りつぶす技がよく分からんので、3次元空間の中の「曲面」の境界面のみを描いております。
draw3d(proportional_axes = xyz, enhanced3d=true, implicit(x^2+y^2+z^2=1, x, 0, 1.5, y, 0, 1.5, z, 0, 1.5))
心の目でx=0, y=0, z=0も境界だと思えば、スイカかメロンを8等分した形が見えてきますわな。スイカかメロンなら緑色に塗りつぶす方法を調べるべきだったか。
空間極座標への変換とヤコビアンさん
上記のグラフ化をすれば(多分、Dの式を見ただけでも分かるケド)これは3Dの極座標変換するとよいことは一目瞭然。以下のように極座標 (r, θ, φ) に変換いたします。地球に例えると、x,y平面が赤道とすると、φが経度、しかしθは北極を0とした角度であります。勿論rは地球中心からの距離ね。
さて、このような時のヤコビアンさんをMaxima様にお願いして求めます。Maximaのjacobian関数は、偏微分した後の行列を求めてくれるところまでで行列式の計算は別です。
行列式の三角関数の整理がメンドイですが、Maxima様の場合 trigrat()関数で一発です。良かった。
さて積分変数を変換した積分は
以上で変数変換の準備ができたので、例によって積分を実施する寸前で止めておく「スンドメ」スタイルでまず積分を書いてから、ev関数で評価して答えを求めてみます。
計算すれば一発だあ。良かった。