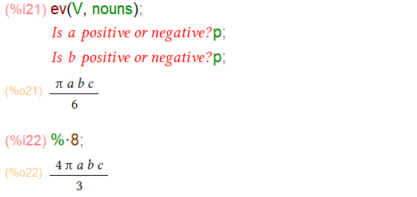頭に霞がかかった年寄デス。前回、二重積分を使って面積を求めたと思ったら、こんどは二重積分で体積を求めろとのお題です。なんだかな~どこかでやったような気もするな~気のせい?例題は楕円体っす。ラグビーボール型、W杯か。楕円ってことは何かい、極座標変換かい。するっていとまたまたヤコビアンさんか、真打登場ってか。
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の教科書(参考書、問題集?)の例題をMaximaの練習に使わせていただいております。
遥かなるかな太古の時代、大学生のときにこういう御本が欲しかったデス。
※以下のMaxima/wxMaximaバージョンで実習させていただいております。
-
- Maxima 5.46.0
- wxMaxima 22.04.0
今回の例題
以下の式でしめされる楕円面で囲まれる部分の体積を「2重積分」を使ってもとめよ、というのがお題です。「楕円体の体積の公式」というものがあるので、ぶっちゃけソレを求めよってことですかい?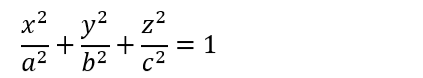
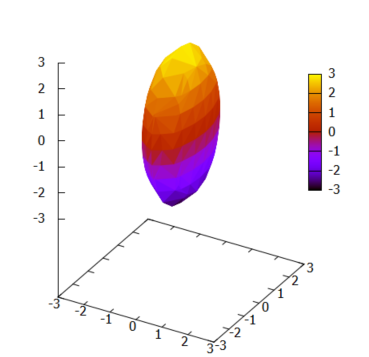
まずは3次元プロットを行って楕円体の雰囲気を味わいたいと思います。例によってグラフ化するためには定数 a, b, c の皆さんに何か具体的な数値を当てはめておかないとならないので、以下のように1,2,3と。なお、a、b、cのうち2つ以上がイコールの関係であると「回転楕円体」に昇格?です。
変数変換と極座標変換
さて、楕円体の雰囲気は分かった(ホントか?)なので、さっさと極座標変換して積分して行きたいと思います。その前に、上記のプロットでa, b, cの皆さんに値を当てはめてしまったのを外します。エイ。
kill()関数とは物騒な。
また、楕円体ということから、上記の図形を縦横に包丁を入れて4分割した上で、「赤道」でさらに2分割してもそれぞれのきれっぱしの体積は一緒だと。よって、8分の1の大きさについて求めていくことにいたします。ここは教科書通りね。
さて、体積を求めるために z について解いてz = の形にいたします。solveすれば一発。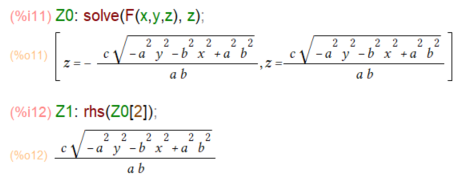
8個の小片のうち、x≧0, y≧0、z≧0の1個の体積を求めようというので解のうちZ1だけ取り出せばよろしかろうと。
さて、極座標に変数変換するついでに、真打、ヤコビアンさんも計算してしまいます。こんな感じ。X、Yが大文字にしてあるのは後で操作をやりやすくするためです。
ヤコビアンさんJが求まりました。
積分すると
最初に先ほど z=の形に書き直してあった x, yの式をX、Y使って変数変換しちまいます。その上でヤコビアンさんJを乗じて、変数変換後の領域
M: 0≦r≦1、0≦θ≦π/2
で積分するとこんな形。
上記は積分記号をあじあうために積分直前で止めたスンドメ形です。
何もassume していなかったのでインタラクティブに問いかけを受けました。また、8分の1の小片を計算していたことを忘れてました。最後に8倍して楕円体の体積の公式が求まりましたです。よかった。