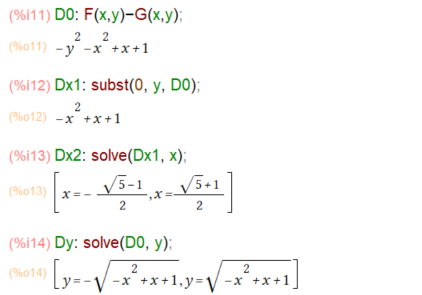今回はフツーに２重積分で体積を求める例題です。前回のように座標変換など出てこないのでヤコビアンさんなどは登場しませぬ。ひたすら「解くのみ」であります。こういう極力頭を使わない力業的な計算においては、Maxima様のご利益は絶大であります。ただただおすがりして計算をお願いするのみ。他力本願。違うか？
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の教科書（参考書、問題集？）の例題をMaximaの練習に使わせていただいております。
遥かなるかな太古の時代、大学生のときにこういう御本が欲しかったデス。
※以下のMaxima/wxMaximaバージョンで実習させていただいております。
-
- Maxima 5.46.0
- wxMaxima 22.04.0
今回の例題
「あたりまえ」っちゃあたりまえな以下の公式？どおりに体積を求めよとのお題です。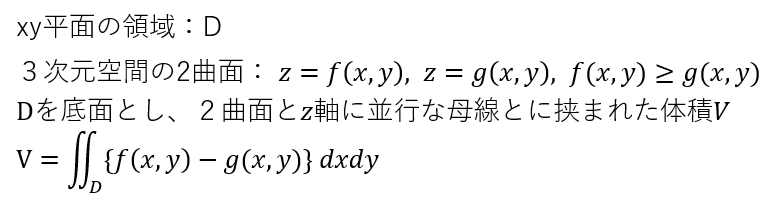
例題としては以下のf(x,y), g(x,y)について体積を求めよと。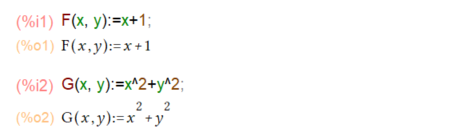
素直で良い感じです。
まずは積分すべき領域を確認
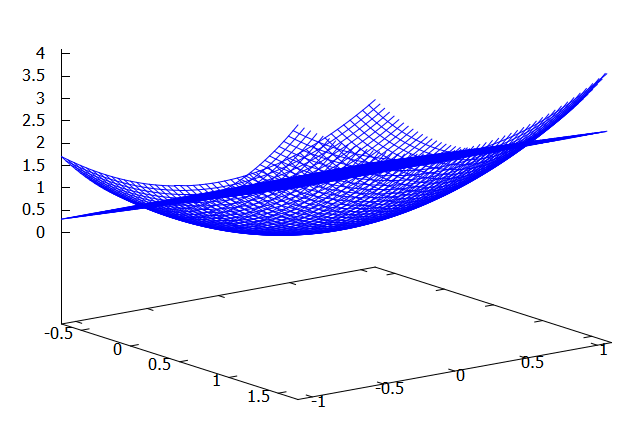
前回のように陰関数ではなく、z=の形の陽関数で問題が定義されているのでグラフを描くのもお楽。
draw3d(explicit(F(x,y),x,-0.7,1.7,y,-1.1,1.1), explicit(G(x,y), x, -0.7, 1.7, y,-1.3,1.3));
描いた３次元図形が以下に
なにやらザルの上を平らな板でふさいだような領域の体積を求めよということみたいです。
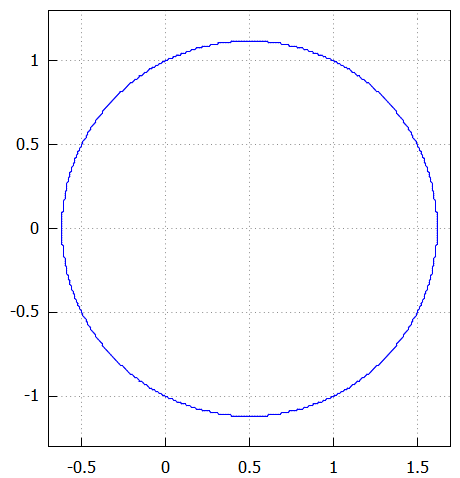
xy平面への正射影も描いておく
頭に霞がかかった年寄でも上記のようにプロットすれば、求めるべき体積のイメージはわくというもの。しかし、具体的に計算をすすめるためには積分領域D、すなわち曲面f(x,y)とg(x,y)の交線をxy平面上に投影した正射影を求めたいです。
まずは２次元平面上でDがどんなもんだか、プロットしてみます。
draw2d(proportional_axes=xy, grid=on, implicit(F(x,y)-G(x,y), x, -0.7, 1.7, y, -1.3, 1.3));
図形は「まる」ね。
計算はこんな感じ。
これで、Dを具体化できたので、いよいよ積分と。
積分して体積を求める
Maxima様にお願いする積分は以下のとおり。いつものように１行目は積分直前で評価を止めて積分記号の姿を味わうスンドメ方式です。２行目のevで値を求めるっと。
I: 'integrate('integrate(F(x,y)-G(x,y), y, rhs(Dy[1]), rhs(Dy[2])), x, rhs(Dx2[1]),rhs(Dx2[2]));
ev(I, nouns);
結果が以下に。
なにやら計算が難し気な感じですが、ひたすらMaxima様にお願いすれば答えは一撃っす。なんの迷いもないっと。ホントか？