今回は「重心を求める」の回です。密度一定の平面図形ですけど。既に忘却の彼方の公式などを、いろいろ思い出しながらお答えと求めていきたいと思います。といって計算するのはMaxima様ですが。計算の例題は冒頭に掲げましたるカージオイド（心臓形）であります。最近は高校の数学Cという科目で習うんだそうな。老人には記憶がないっす。
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の教科書（参考書、問題集？）の例題をMaximaの練習に使わせていただいております。
遥かなるかな太古の時代、大学生のときにこういう御本が欲しかったデス。
※以下のMaxima/wxMaximaバージョンで実習させていただいております。
-
- Maxima 5.46.0
- wxMaxima 22.04.0
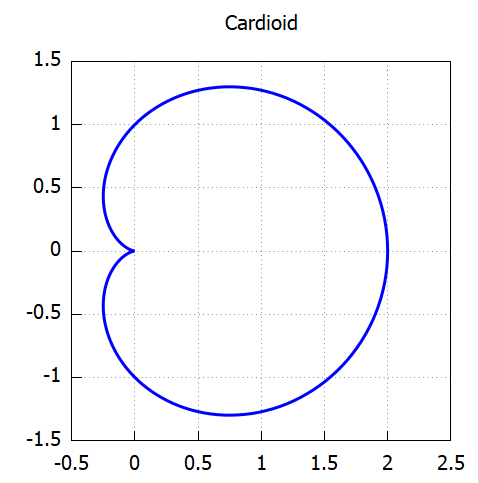
カージオイド r=a*(1+cos(θ)) (a>0)
案ずるより産むがやすし（意味がチガクないか？）ということでMaxima様にプロットしていただきます。例によって定数の値を決めないとグラフに描けないので、aは１にしておきまする。
a: 1; draw2d(user_preamble = "set grid polar", proportional_axes=xy, grid=on, nticks = 200, xrange = [-0.5, 2.5], yrange = [-1.5,1.5], color = blue, line_width = 3, title = "Cardioid", polar(a*(1+cos(θ)),θ,0,2*%pi ))
プロットしたものが以下に。
今回、極座標プロットをすることをMaxima様はお見通しだったみたいっす。立ち上げたときに表示される Tip of the dayはこんなんでした。さっそく set polarしてみたと。
なお、極座標プロットの方法を含むMaxima様の日本語マニュアルページは以下に。
平面図形の重心を求める式
平面の密度に変化がある場合の重心は密度関数ρを使って以下のようになるみたいです。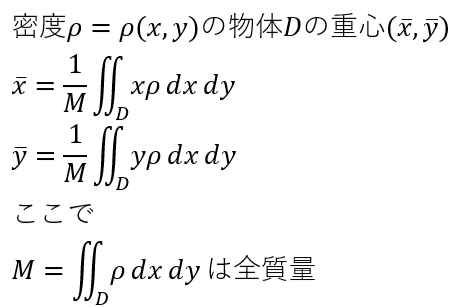
一方、密度一定の場合は簡単になって以下だと。
ともかく、密度一定なら面積もとめて、二重積分した結果を割れば重心位置が求まるのね。。。
カージオイドの面積を求める
まずは面積Sから求めてみます。過去回でやっている筈なのだけれど、極座標r=f(θ)で定義された曲線の面積の求め方は以下のとおり。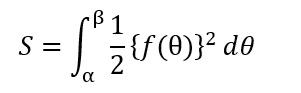
Maxima様へのお願いの筋は以下で。
F(θ):=a*(1+cos(θ)); S0: 'integrate((1/2)*F(θ)^2, θ,0,2*%pi ) S: ev(S0, nouns);
実際に実行してみるとSが求まります。
重心の式を極座標変換、積分
上にあげた重心を求める式は x, y でした。一方例題は極座標表示です。極座標の式とともに、久しぶりに極座標変換したときのヤコビヤンさんも求めてみます。
上記を使って重心の座標を求めますが、ここで図形の対称性から重心のy座標はy=0に決まっておるので、x座標のみ計算するっと。計算はこんな感じ。
XB0: 'integrate('integrate(x*J, r, 0, a*(1+cos(θ))), θ, 0, 2*%pi);
XB1: ev(XB0, nouns);
XB: XB1 / S;
実行したところが以下に。
重心の座標は(5a/6, 0)ってことですかい。