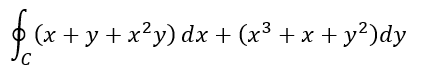奥底で渦をまく者どもを引っくくって積分すればあら不思議、表に見えている何やらをまるっと積分するのと等価だと。ストークスの定理は「ベクトル解析業界」の一丁目一番地かもしれません。今回はそんなストークスの定理の手前の平面にいるらしいグリーンの定理を練習してみます。Maxima様に計算をお願するだけだけれども。
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の教科書(参考書、問題集?)の例題をMaximaの練習に使わせていただいております。
遥かなるかな太古の時代、大学生のときにこういう御本が欲しかったデス。
※以下のMaxima/wxMaximaバージョンで実習させていただいております。
-
- Maxima 5.46.0
- wxMaxima 22.04.0
Greenの定理
ネット上では偉い先生がたがいろいろ説明されているので、数学素人の老人は何も言いますまい(というか、説明しろと言われたらしどろもどろ。)ご参考のため、いつもお世話になっております『高校数学の美しい物語』様の以下のページへのリンクを貼らせていただきます。
ついでにもう一つリンクを貼らせていただきます。
今回「まるっと」積分するのはC1級関数ということで。
一応、備忘のためグリーンの定理、ストークスの定理の公式のみ以下に貼り付けておきます。これを見ながらMaxima様にお願いすれば一発だ、と。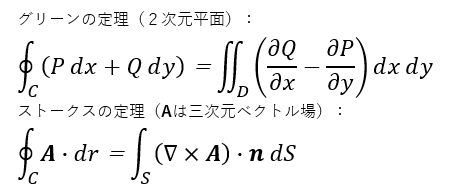
今回の例題
有界な領域Dの境界が、閉曲線Cのとき。。。ということでまずは閉曲線Cはぶっちゃけ円です。単純明快。
C: x2+y2=a2 (a > 0)
一応この円をプロットしておくと以下のようです。例によってプロットするためにaには具体的な数値1を当てはめてあります。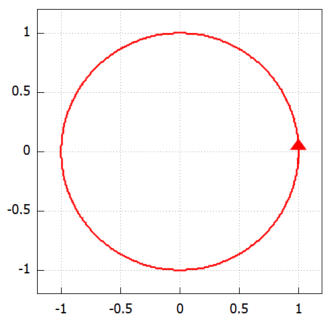
キモは「矢印」ですな。積分するときは円の内部を左に見て回れっと。ちなみに上記を描くために、Maxima様には以下のようにお願いしています。
s0: [1, -0.1]; e0: [0, 0.2]; draw2d(proportional_axes=xy, grid=on, head_length = 0.2, head_angle=20, line_width = 2, color = 1, vector(s0, e0), implicit(x^2+y^2-1, x, -1.2, 1.2, y, -1.2, 1.2) );
グリーンの定理を適用
上の問題からP、Qを宣言し、そして二重積分の中に入る(∂Q/∂x)-(∂P/∂y)を準備しておくと以下のようです。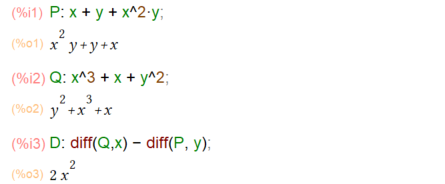
さて積分範囲は円Cの上から、円の面積Dになるのですが、計算しやすくということで極座標形式に変換します。円だけに。(x, y)から(r, θ)に座標変換するので例によってヤコビアンさんを求めておくとこんな感じ。
お答えが求まりました。お作法どおりか?