微分方程式のHelloWorld的例題の練習4回目です。前回は単振動のモデル、物理現象に対応しているので分かりやすかった?今回は微分方程式の解が表す曲線(解曲線)の全体は平面全体を覆うことが「多い」の回デス。プロットして「味わってみるだけ」だけれども。まあ10本も解曲線を引いてお茶を濁しますです。
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の教科書の例題をMaximaの練習に使わせていただいております。ただし御本家『培風館』様のホームページで検索してみるも掲載されていないようです。絶版? そのため以下のリンクは『Amazon』の通販ページであります。ご注意を。
※MaximaおよびそのGUIであるwxMaximaの以下バージョンを使用させていただいております。
-
- Maxima 5.46.0(x86_64-w64-mingw32)
- wxMaxima 22.04.0
今回の例題
例題の微分方程式自体は簡単、解くのも簡単(実際に解いているのはMaxima様だけれども)です。
ここで任意定数Cを「実数全体」で変化させると、Y(t)が表す曲線はY-t平面全体を覆うみたいです。知らんけど。逆に言えば、曲線群が共通に満たす「関係式」が上記の微分方程式の解であると。
プロットするしかありますまい
とはいえプロットするには具体的な数値をあたえなければなりません。被プロット関数(微分方程式の解)を以下のように定義し、任意定数Cに対して具体数値リストを与えてプロットする操作が以下に。
f(t, C):=C*%e^(2*t); plot2d(makelist(f(t, C),C, 1, 10), [t, 0, 3]);
そのプロット結果が以下に。10本くらいじゃ、全然平面を埋め付くせた感じがしない。それに横軸と縦軸のスケールがあまりに違いすぎるのも難点。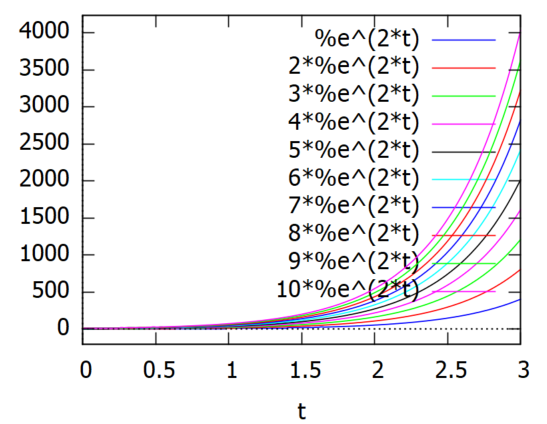
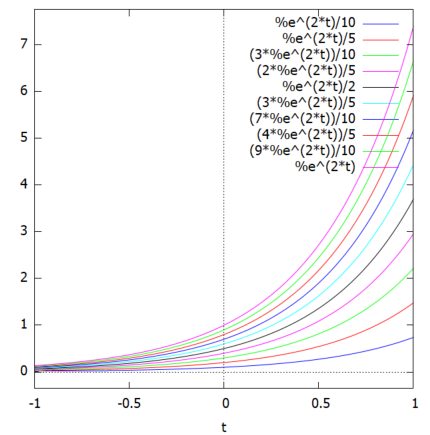
そこでパラメータとしてのCを10分の1にして(任意定数だから、何分の1にしようと御勝手)、プロット範囲を狭めた上に、縦横のスケールを1:1にしたものが以下です。
g(t, C):=(C/10)*%e^(2*t); plot2d(makelist(g(t, C),C, 1, 10), [t, -1, 1], [yx_ratio, 1]);
縦軸、横軸の範囲を大分変えたのだけれど遠くから見たら結局一緒だあ。元の数式が一緒だから、スケールを変えても見えるものは同じか。