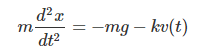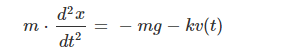別シリーズで年甲斐もなく微分方程式の解き方をMaxima様に教わっている年寄です。今回は、Googleの生成AI、Gemini様にまた茫漠とした問いかけをしてしまいました。「地表面における空気抵抗を含んだ落下の微分方程式を立ててください」と。Gemini様のお答えは年寄の予想外に「深い」ものでありました。流体力学よ。
※Google様の生成AI、Gemini（無料プランだけれども）を使って回路を設計してもらっています。
別件シリーズで活躍するode2
ode2関数は、皆大好き無料の数式処理ソフトウエアMaximaで１階、２階の常微分方程式を解くための関数です。ode2に微分方程式を渡せばするすると一般解が求まってしまう強力な関数です。ただし、残念ながら微分方程式を「たてる」ことはしてくれません。あたりませか。
それならばGoogleの生成AI、Gemini様に微分方程式をたててもらえば、いいんじゃね、と短絡。さっそくプロンプトに投げかけてみたのが以下の１文であります。
地表面における空気抵抗を含んだ落下の微分方程式を立ててください
これを投げかけたとき、頭の固い老人の頭にあったのは「空気抵抗は速度に比例するから。。。」という１点であります。しかし、Gemini様の回答はそんな想定を超えてました。
数式の表示に使わせていただいたサイト
今回、Gemini様は数式を表すのに数式の「文字列表現」を使ってます。それを美麗な数式に表現してもらうのに以下のサイトを使わせていただきました。あざーす。
Gemini様のご回答３案
Gemini様は例によって３案併記してくれますが、前回のマイコンにメモリを接続してね、とお願いしたときの自信なさげな回答と比べると、今回は「自信に満ち溢れた」感じがします。数学は得意分野なのね。。。
以下は茫漠とした問いかけをした老人の勝手な感想です。
-
- 回答案１
微分方程式、その解き方、一般解、終端速度など当方想定のほぼ全てを網羅していただけている充実した内容じゃないかと思います。途中出てくる数式は Latex式の表現形です。こんな感じ。
m \frac{d^2 x}{dt^2} = -mg - kv(t)
HostMath様により画像化したものが以下に。
-
- 回答案２
数式表現はAsciiMath？知らんけど。まあLatex式よりはお手軽な感じっす。Gemini様の出力は以下のようです。
m * d^2x / dt^2 = -mg – kv(t)
当方で勝手にちょいカッコでくくったものが以下に。
m * (d^2x) / dt^2 = -mg - kv(t)
上記をHostMathに画像化していただいたものが以下に。
なお、回答案２では空気抵抗について以下のような記述がありました。
この記述は、当方想定の範囲内です。なお、回答案２では微分方程式を解析的に解くのは難しいから、数値解法使えやとのお言葉あり。実用的？投げやり？
-
- 回答案３
回答案３の数式もAsciiMath的表現だったですが、老人の想定を超えてきました。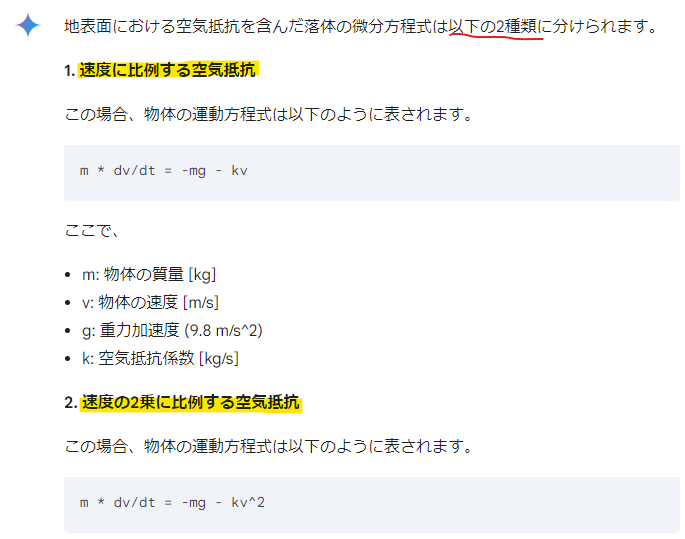
前者は粘性抵抗、後者は慣性抵抗（ニュートン抵抗？）ということになるのかと思います。落下する物体の形状が弾丸みたいな形で十分に重ければ後者の式になってくるのかと思います。どうもレイノルズ数によってドッチになるか決まるみたい。流体力学やな～。遥かな太古の時代、流体力学習ったハズ、完全に失念しておりました。これだけでもGemini様に問いかけたかい（解？）があるものと。
Gemini様に立ててもらった微分方程式をMaxima様に解いていただく
２階になってしまうx（位置）についてではなく、１階で済むv（速度）についての以下の微分方程式（回答案１で「変数分離形」として記されているもの）を解いてもらうことにいたしました（お楽だし。）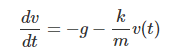
Maxima上で上記を解いたものが以下に（Gemini様も解は示しているんだけれど。）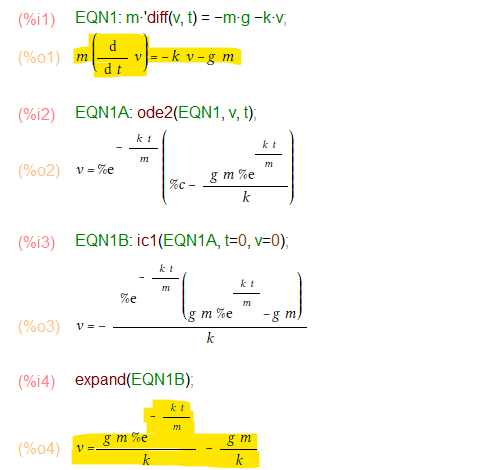
やっぱり、ode2で一撃必殺。