前回はIIRフィルタの設計に「使えそうな」設計関数を列挙。その上で以前に使用したことのあるiir()関数をおさらいしてみました。アナログフィルタを双一次変換して離散的なデジタルフィルタにする関数ね。今回はeqiir()関数を練習してみます。歴史と伝統？の計算アルゴリズムsyredi関数のフロントエンドみたいです。
※「手習ひデジタル信号処理」投稿順 Indexはこちら
※Windows11上で、Scilab6.1.1およびScilab上のツールボックス Scilab Communication Toolbox 0.3.1（以下comm_tbx)を使用させていただいとります。
eqiir()関数
eqiir()関数は、sysredi()関数のフロントエンドみたいです。その心？はsysredi()関数の引数が余りに飾り気のない数値の連続なので、多少なりとも「分かり易く」してみた、というところみたい。知らんけど。よって計算アルゴリズム的にはsysredi()関数と同一。sysredi()関数についてはHELPみると以下のように注釈がありました。１か所引用させていただきます。
syrediコードは,Guenter F. Dehner, Institut fuer Nachrichtentechnik Universitaet Erlangen-Nuernberg, Germany により書かれたdorediパッケージから 派生したものです.
1979年にFORTRANで書かれたコードみたいです。ほぼ５０年近くの風雪？に耐え、今だに使われているのは立派な証拠？
御本家のeqiir関数の解説ページは以下です。
確かにsysredi()関数の引数と比較するとかなり「分かり易い」感じがしないでもないです。しかし前回のiir()関数などと比べると、信号処理素人にはハードル高いです。具体的な引数については上記を御参照いただくとして、注意点としてはカットオフ周波数の指定が１か所につき１点ではなく２点（通過域と阻止域の目印だと思います、バンドパス、バンドストップでは２点ｘ２か所で４点）必要であることと、角周波数（離散フィルタなので正規化）rad/sで指定することです。
パラメータによりどんなフィルタが出来るのか分からないので、テキトーにパラメータを「振って」振幅特性を拾ってみました。いずれもバタワースなローパスフィルタで、前回 iir関数のときに生成したものと似せてます。
第１のケース
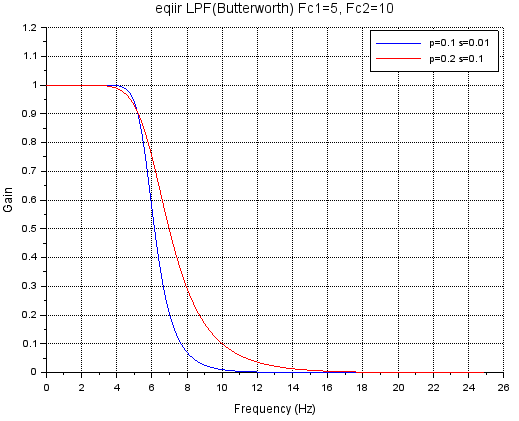
「カットオフ」の下側5Hz、上側を10Hzとしてサンプリング周波数50Hzで正規化した角周波数で指定した場合の計算です。通過域と阻止域のリップルを制御するパラメータ deltapとdeltasの値を変化させた２つについてグラフを描くためのコードとしてあります。
Fs=50;
Fc1=5;
Fc2=10;
Wcut=(Fc1/Fs)*2*%pi;
Wcut2=(Fc2/Fs)*2*%pi;
[cellsA,factA,zzerosA,zpolesA]=eqiir('lp','butt',[Wcut,Wcut2],0.1,0.01)
[cellsB,factB,zzerosB,zpolesB]=eqiir('lp','butt',[Wcut,Wcut2],0.2,0.1)
hA=factA*poly(zzerosA,'z')/poly(zpolesA,'z')
hB=factB*poly(zzerosB,'z')/poly(zpolesB,'z')
[hzmA,frA]=frmag(hA,256);
[hzmB,frB]=frmag(hB,256);
clf();
plot2d(frA'*Fs,[hzmA', hzmB'], [2, 5]);
xtitle('eqiir LPF(Butterworth) Fc1=5, Fc2=10');
xgrid();
xlabel("Frequency (Hz)");
ylabel("Gain");
legend('p=0.1 s=0.01', 'p=0.2 s=0.1');
上記のコードで得られた周波数特性が以下に。
なお、このときに eqiir()関数が返してくる生の値が以下に。
上記の値から決まる離散的な複素伝達関数が以下に。
第２のケース
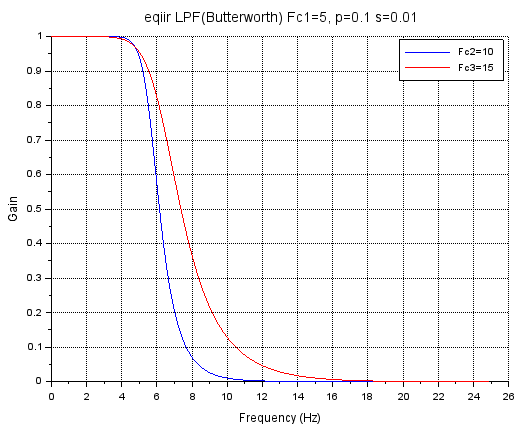
「カットオフ」の下側5Hzは同じで、上側を10Hzと15Hzの２例で再計算した場合です。15Hzにすれば「ゆるやか」な特性になる期待。コードが以下に。
Fs=50;
Fc1=5;
Fc2=10;
Fc3=15;
Wcut=(Fc1/Fs)*2*%pi;
Wcut2=(Fc2/Fs)*2*%pi;
Wcut3=(Fc3/Fs)*2*%pi;
[cellsA,factA,zzerosA,zpolesA]=eqiir('lp','butt',[Wcut,Wcut2],0.1,0.01)
[cellsB,factB,zzerosB,zpolesB]=eqiir('lp','butt',[Wcut,Wcut3],0.1,0.01)
hA=factA*poly(zzerosA,'z')/poly(zpolesA,'z')
hB=factB*poly(zzerosB,'z')/poly(zpolesB,'z')
[hzmA,frA]=frmag(hA,256);
[hzmB,frB]=frmag(hB,256);
clf();
plot2d(frA'*Fs,[hzmA', hzmB'], [2, 5]);
xtitle('eqiir LPF(Butterworth) Fc1=5, p=0.1 s=0.01');
xgrid();
xlabel("Frequency (Hz)");
ylabel("Gain");
legend('Fc2=10', 'Fc3=15');
特性が以下に。
第３のケース
「カットオフ」の上下を並行移動したらグラフは「右にシフト」する筈。コードが以下に。
Fs=50;
Fc1=10;
Fc2=15;
Wcut=(Fc1/Fs)*2*%pi;
Wcut2=(Fc2/Fs)*2*%pi;
[cellsA,factA,zzerosA,zpolesA]=eqiir('lp','butt',[Wcut,Wcut2],0.1,0.01)
[cellsB,factB,zzerosB,zpolesB]=eqiir('lp','butt',[Wcut,Wcut2],0.2,0.1)
hA=factA*poly(zzerosA,'z')/poly(zpolesA,'z')
hB=factB*poly(zzerosB,'z')/poly(zpolesB,'z')
[hzmA,frA]=frmag(hA,256);
[hzmB,frB]=frmag(hB,256);
clf();
plot2d(frA'*Fs,[hzmA', hzmB'], [2, 4]);
xtitle('eqiir LPF(Butterworth) Fc1=10, Fc2=15');
xgrid();
xlabel("Frequency (Hz)");
ylabel("Gain");
legend('p=0.1 s=0.01', 'p=0.2 s=0.1');
特性が以下に。
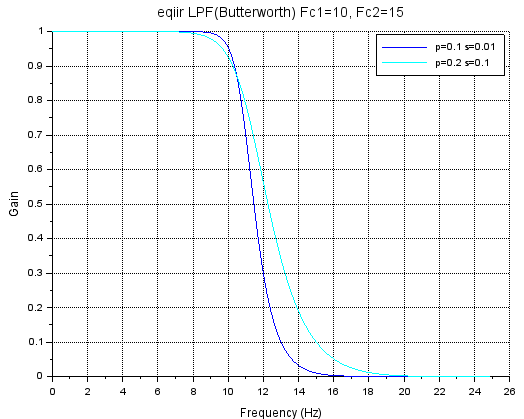なんとなく制御できているような、いないような。信号処理素人には敷居が高いデス。