前回までの「連続時間」パレット内のブロックでは信号は連続の「てい」でソルバ様に計算(積分)されとりました。しかし今回からの「離散時間」パレット内では、アカラサマにトビトビの時間に対して計算されます。連続時間のときの「s」ではなく「z」が登場。まあ、ムツカシーことは言わないでも計算はできるっと。いいのか?
※「ブロックを積みながら」投稿順 index はこちら
※動作確認にはWindows 11のパソコン(64bit)上にインストールしたScilabの以下バージョンを使用しています。
Scilab 2024.0.0
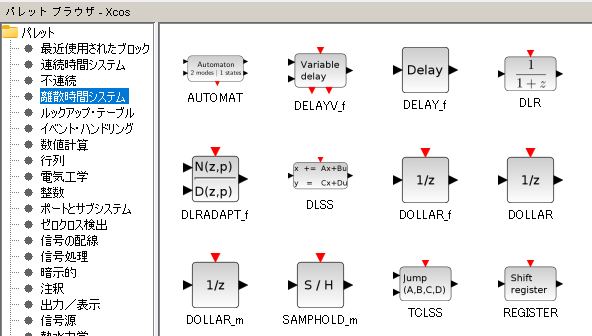
離散時間(Discrete time systems)パレット
「離散的な信号を処理するための」ブロックどもが並んでます。ぶちゃけ、離散的な信号って何よといえば、サンプリングされたデジタル信号ということでよろしいでしょうかね?そして、それらの処理は 差分方程式 で書かれることになります。一例が以下に。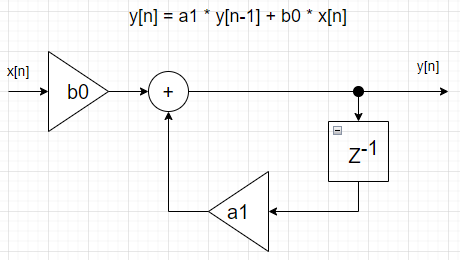
上の例での、現時点の出力信号 y[n] は、一個前の時点の出力信号y[n-1]に係数 a1 を乗じたものと、現時点で入力されてきている入力信号 x[n] にb0を乗じたものを加え合わせたもんだと。
差分方程式が上部に掲げられており、下の丸と三角と四角がブロック図ということになります。恐ろしいことに丸と三角と四角で世の中大抵のものは書けてしまうっと。。。知らんけど。
丸と三角と四角で描いたブロックダイアグラムのアレコレについて、別件記事でちょっとまとめたものが以下に。
手習ひデジタル信号処理(126) FIR、IIR、直接形、転置型、継続形ブロックダイアグラム
そして信号処理素人老人には人の受け売りです。上記のブロックダイアグラムの表す伝達関数は「z変換」にて以下のようにかけるっす。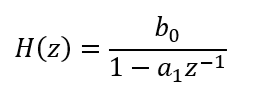
遅延演算子 z-1
ここまで度々登場している z-1 はムツカシーことを踏みにじってしまえば「遅延素子」であります。差分方程式上の [n-1] などに相当する「1個前の値」を参照するためのもの。これを並べていけば、1個前だろうが、2個前だろうが思いのまま。そしてコンピュータや電子回路上での実現は記憶素子で済むっと。お惚け老人にも回路は作れます。
そのためなのかは知らず、離散時間パレットをよく見ると以下のように z-1 (1/zということだね)が多数ならびたってます。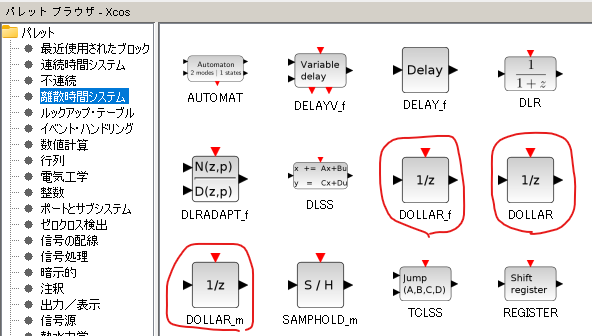
Xcos(昔のお名前はScicos)あるあるですな。きっと歴史的な事情があるのでしょう、同名のブロックの複数並立。多分「中の人」も問題に思ったのでしょう、以下のページに表があります。
上記の 「1/z」なやつらについては以下のように分類されております。
-
- Deprecated block (or scheduled for deprecation)
DOLLAR
DOLLAR_f - Suggested replacement block
DOLLAR_m
- Deprecated block (or scheduled for deprecation)
つまり前の2つは「非推奨(もしかすると将来なくなる)」、最後の奴を使えってこってしょうか。しかし、離散時間パレットの以下の解説ページ(最新版の2024デス)を見ると、解説されているのはDOLLAR_fです(コマケー話だけれど_fのfはFORTRANのfでないかしらん。)
この辺の首尾一貫しないところもScilab/Xcosらしいっちゃらしいっす。まあ、いまのところどれでも使えるみたい。どれでもいいか。
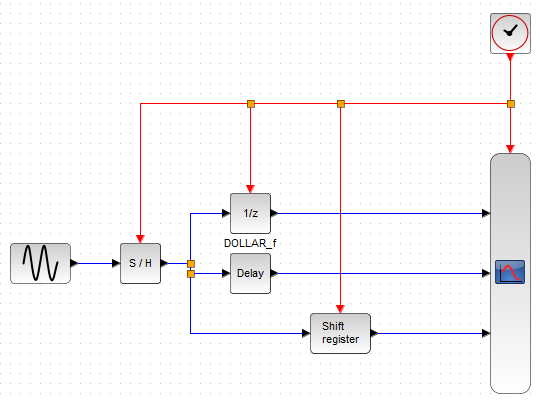
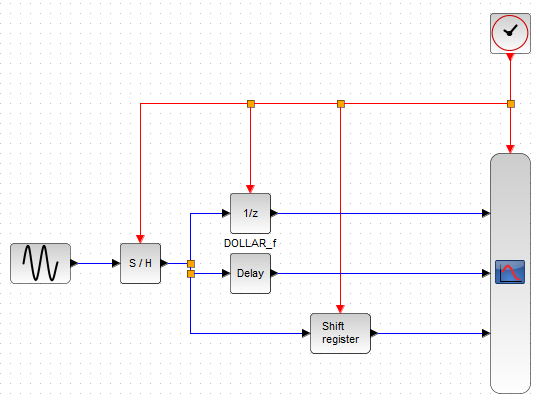
今回実験のフロー
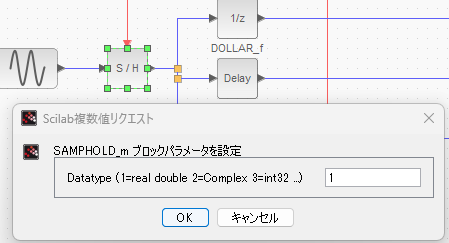
信号源は「連続時間」側の正弦波生成ブロックです。ここからSIN波が到来しますが、それをS/H(サンプル&ホールド)ブロックでサンプリングします。サンプリングクロックは上にあるCLOCKブロックから同じ信号を皆に配ってます。念のため正弦波生成ブロックの設定が以下に。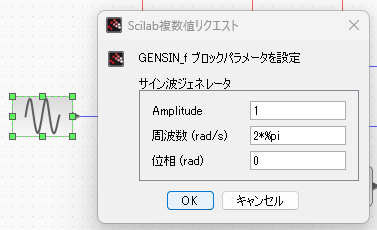
さて、サンプル&ホールド・ブロック通過後の「離散的な」信号が、「1/z」と「Delay」と「Shift register」という似たような機能のブロック共に入力されるのを眺めてみよう、というのが今回の趣旨であります。
グラフは「サンプリング・クロック」次第ね
さて観察できる波形はCLOCK_cブロックに設定するサンプリング間隔次第です。元の「連続」波形は周期 2Π[rad/s]つまり1Hzです。まずは0.1s毎(10Hz)のサンプリングの場合。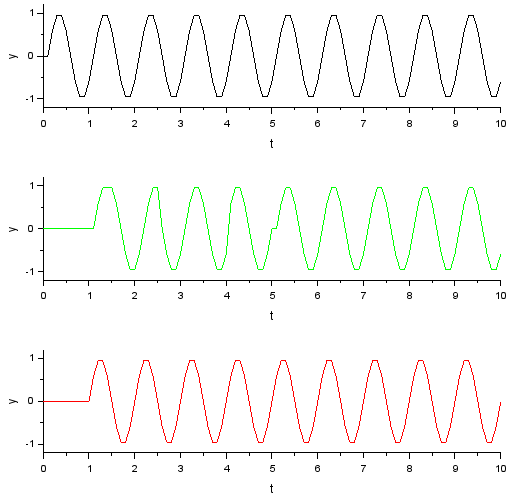
一番上の黒が「1/z」による遅延です。一拍(0.1s)遅れて入力の正弦波波形が現れているように見えます。下の緑と赤はDelayとShift registerです。緑はクロック信号とはかかわりなく内部に保持するタイミングでシフトレジスタ相当の遅延を行うもの。赤の方は外部からもらったクロック信号で遅延させるものです。
赤の方は固定した遅延でその挙動は明朗なのだけれども、緑の方は、ところどころなんでズレるのか良く分かりませぬ。何か内部に大人の事情でもあるのか。。。
つづいてサンプリングを0.25s(4Hz)としてみます。こんな感じ。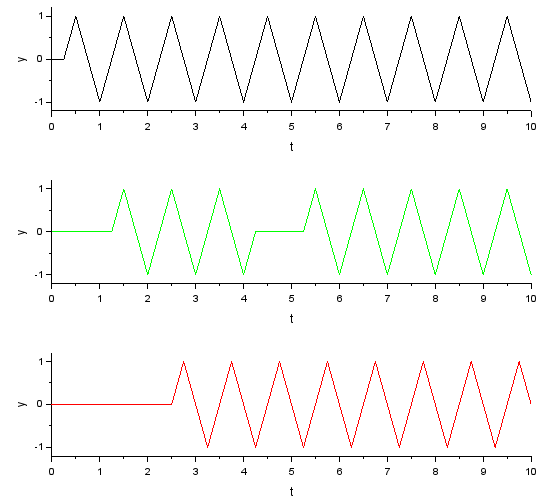
三角波になっちまいました。元の波形の周波数 1Hz は残っているけど、正弦波の形は失われとります。
つづいてサンプリングを0.5s(2Hz)としてみます。1Hzの信号にとっては泣く子も黙る「ナイキスト周波数」まで落としてしまいました。そしたら、こんな感じ。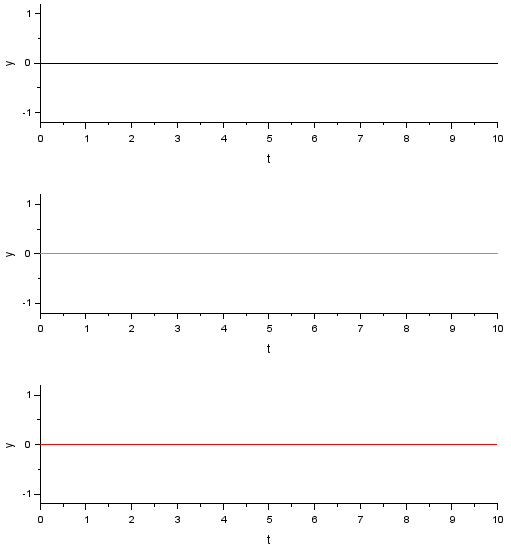
ダメじゃん、お亡くなりです。ピッタンコなナイキスト周波数では元の周波数が失われてしまいますなあ。離散時間よ。