Rのパッケージ「Boot」のサンプルデータセットをabc順に経めぐってます。前回、実験動物の皆さまは多分ほぼ確実にお亡くなりのハズ。今回も生物相手の実験データです。なんとアカラサマに毒に晒してからの対処方法による生存時間の違いを測ったデータみたいです。結局皆お亡くなり？実験対象が何だとかは言及ないけど冷酷な科学の進歩？
※「データのお砂場」投稿順Indexはこちら
生死の判定の時間
忘却力の老人も「LD50」という言葉を覚えております。朧げな記憶によれば、毒を生き物に投与した場合に半数が死亡する分量を示す値。当然小さい値ほど猛毒となる筈。今回のデータセットは毒の分量についてはまったく言及ないので、LD50とは関係ないのですが、今回死亡までの時間のデータセットを見ていて気づいてしまいました。
LD50での生死の判定は「何時間後なのか」という問題です。即効性の場合もあれば、じわじわ効く（恐ろしいなあ）ものもあると想像されるからです。調べてみたら、以下の文献にあたりました。『植物防疫 第24巻10号 植物防疫基礎講座』様
上記は植物についてくる害虫どもを燻蒸したりするための処置を念頭においた解説のようですが、２４時間もしくは４８時間という時間を上げてました。
なおよく見かける？LD50のグラフについて、上記文献は「シグモイド曲線」であると述べています。なぜか懐かしい「シグモイド曲線」、ニューラルネットのコンボリューションの「ピラミッド」の末尾に鎮座するシグモイド関数がメンドイなどと思った記憶が蘇ります。閑話休題。
なお、今回は関係ない LD50 の算出方法については以下も拝見させていただきました。
なお、上記からＲ言語で記述されたLD50を計算可能な関数ソースへのリンクがあります（群馬大様）
ED50はLD50とは方向が１８０°異なる（お救いする方向）数値ですが、同一の算法で求まるみたいです。
poisonsサンプルデータセット
サンプルデータセットの解説ページが以下に
具体的に何とは書かれていない３種類の「毒」を具体的に何とも書かれていない生物に投与後、これまた具体的に何とは書かれていない４種類の「処置方法」で何時間（単位は10時間）生存していたのかを記録したデータセットです。３ｘ４で１２種類の条件にたいして各４（なんと呼んでよいのか単位は不明）の生物で実験しているので合計４８点のサンプルデータセットです。数字は冷酷にして非情。
先ずは生データ
さて冷酷にして非情なデータをロードしてみたところが以下に。
timeとかかれているのが、生存時間（単位10時間）です。ほとんど単位時間まで生き延びているケースが無いっす。キビシー。
aggregateで層別集計
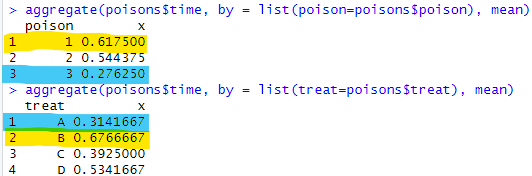
例によって、aggregate関数で層別に集計してみます。まずは単独要因。
aggregate(poisons$time, by = list(poison=poisons$poison), mean) aggregate(poisons$time, by = list(treat=poisons$treat), mean)
集計結果が以下に。
上が三種の「毒」の生存時間の平均で、下が四種の「処置」の生存時間の平均です。黄色のマーカはもっとも「延命」的なもの、青のマーカはもっとも「致命」的なものっす。
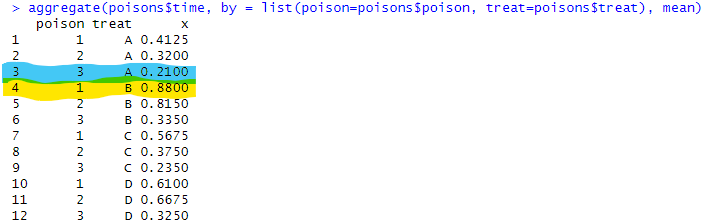
以下は２つの要因を組み合わせてaggregateした場合。
aggregate(poisons$time, by = list(poison=poisons$poison, treat=poisons$treat), mean)
結果が以下に。
単独要因からも見えたとおり、毒３と処置Aの組み合わせがもっとも「致命的」で、毒１と処置Bの組み合わせがもっとも「延命的」（といいつつ最終的にはお亡くなりだけれども）に見えます。
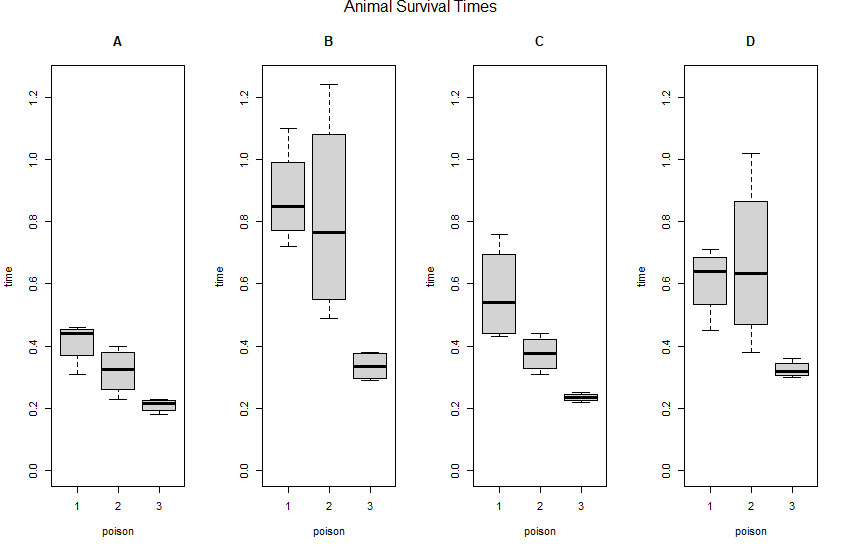
上記の様子をプロット
数値だけだとイマイチなので、以下のようにしてプロットしてみました。
par(mfrow=c(1,4), oma=c(0,0,1.1,0))
plot(time~poison, data=poisons, subset=treat=="A", main="A", ylim=c(0, 1.25))
plot(time~poison, data=poisons, subset=treat=="B", main="B", ylim=c(0, 1.25))
plot(time~poison, data=poisons, subset=treat=="C", main="C", ylim=c(0, 1.25))
plot(time~poison, data=poisons, subset=treat=="D", main="D", ylim=c(0, 1.25))
mtext("Animal Survival Times", side=3, outer=TRUE)
プロット結果が以下に。
２元配置の分散分析
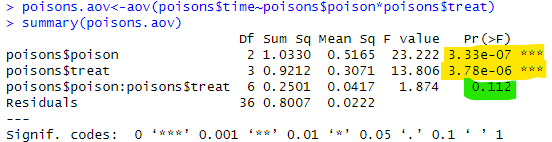
要因は「毒」と「処置」の２つなので、わけも分からないまま、aov関数を使って２元配置の分散分析を試みた結果が以下に。大丈夫か？
poisons.aov<-aov(poisons$time~poisons$poison*poisons$treat) summary(poisons.aov)
結果が以下に。
黄色の２行のところは、P値がとても小さいので、「毒要因による生存時間に違いなどない」という帰無仮説は却下、「処置要因による生存時間に違いなどない」という帰無仮説も却下ということで良いのかな。
しかし、下のところは0.05よりはデカイ数値が入っているので「毒要因と処置要因の組み合わせ、による生存時間に違いなどない」という帰無仮説は却下しきれん、ということか。知らんけど。