信号波形を処理した結果をグラフで見るのも良いのですが「実体験」したいです。それには音にして耳で聞くという方法もありかと。音声データの入出力は第96回、第97回で練習済。今回は処理対象の「音源」として救急車のピーポー音(サイレン)を作製してみましたぞ。一応、ドップラー効果あり、距離減衰あり。なんちゃってだけど。
※「手習ひデジタル信号処理」投稿順 Indexはこちら
※Windows11上のScilab6.1.1およびScilab上のツールボックスを使用させていただいております。
救急車のピーポー音
「ドップラー効果」の例として、必ずあげられる救急車のピーポー音(サイレン)です。調べてみると、960Hzと770Hz、各0.6秒ごとの繰り返しだそうです。そして法令により『車両の前方20m、高さ1mの位置において90dB以上120dB以下』と規定されているみたいです。かなりデカイ音量デス。
そのような大音量を発生するのもはばかられる(手元のパソコンじゃ無理っす)ので、波形の最大振幅を±1.0とした信号として
-
- 前方50m にいる救急車がピーポーと鳴らしながら
- 時速60km/hの速度で
- 静止した観察者に向かって突進してきてその脇をすり抜ける
様子を後で掲げるScilabプログラムで模擬した音が以下であります。
雰囲気でてますかねえ?
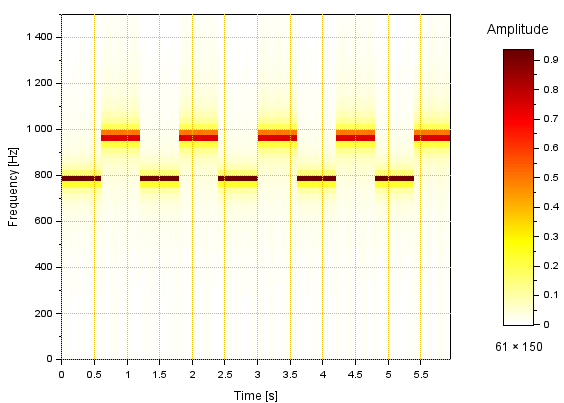
観察者位置を「すり抜ける」ところがイマイチなんでありますが、上記波形のFFT結果は以下のようです。近づくところと遠ざかるところで周波数が変わるので合計4周波数が見えてます。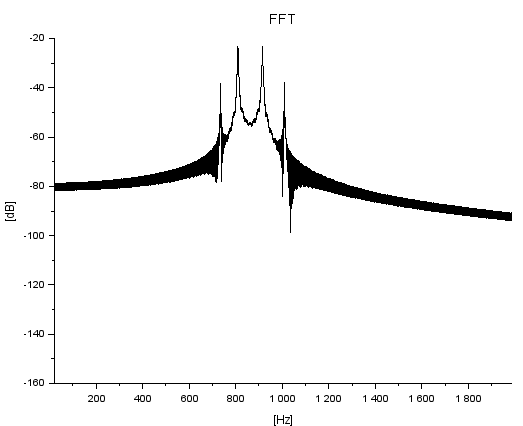
ピーポー音のスクリプト
基本的には「いつもの」正弦波生成と同じなのですが、
-
- 音源が観察者方向に向かってくる速度 vs [km/h]
- 観察者の速度 v0 [km/h]
- 音源と観察者間の距離 [m]
という3つのパラメータが追加されています。なお音源の進行が観察者方向であるときプラス。観察者が音源に向かって対向方向に進んでいるならマイナスです。ドップラー効果を計算するには大気中の音速が必要ですが、気温15℃、標準大気圧のときの値をキメウチで参照してます。また波形の振幅は距離1mのところでサチル設定で、その時の最大振幅を1.0としてあります。
// Sound Source: Ambulance
// Fs: sampling frequency [Hz]
// nSample: number of samples
// vs: sound source speed[km/h]
// v0: observer speed[km/h]
// dist: initial distance between source and observer [m]
// NOTE: Sound Level will be saturated under 1 [m]
function y=ssAmbulance(Fs, nSample, vs, v0, dist)
T06 = int(0.6 * Fs);
vsM = vs * 10^3 / 3600;
v0M = v0 * 10^3 / 3600;
AIR15=340.7;
dopplerAIR15=(AIR15-v0M)/(AIR15-vsM);
fqH = 960 * dopplerAIR15;
fqL = 770 * dopplerAIR15;
mag = 1.0;
cnt = 0;
flag = %T;
for idx = 1:nSample
timeNow = idx/Fs;
distNow = dist - (vsM-v0M)*timeNow;
if flag & (distNow < 0) then
dopplerAIR15=(AIR15+v0M)/(AIR15+vsM);
fqH = 960 * dopplerAIR15;
fqL = 770 * dopplerAIR15;
flag = %F;
end
if abs(distNow) < 1 then
distNow = 1;
end;
magNow = mag / abs(distNow);
cnt = cnt + 1;
if cnt > T06 then
cnt = 1 - T06;
end;
if cnt < 0 then
fq=fqH;
else
fq=fqL;
end;
y(idx) = magNow * sin(2*%pi*fq*(idx/Fs));
end;
endfunction
波形の生成
さきほどのサンプル音声を生成するときのスクリプトが以下に。
Fs=22050;
y=ssAmbulance(Fs, Fs*6, 60, 0, 50);
playsnd(y, Fs);
savewave("ssAmbulance.wav", y, Fs);
なお playsnd()関数で、生成したばかりの波形を音にして聞くことができます。また、savewave()関数でファイル出力しています。
音源が動かず、観察者も動かず、音源距離1mのときの様子を聞くためには以下のようにします。
y0=ssAmbulance(Fs, Fs*6, 0, 0, 1); playsnd(y0, Fs); clf; plotFFT2(Fs, y0', 1);
上記のFFTの結果が以下に。ドップラー効果の影響が無いので周波数のピークは2つだけです。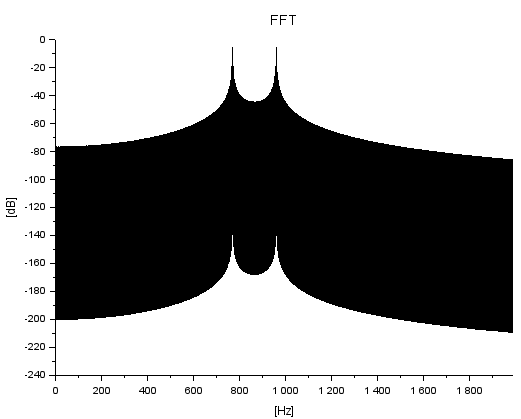
mapsound()関数を使うと、スペクトログラムを生成することができます。操作はこんな感じ。
clf; mapsound(y0, 0.04, 1500, Fs);
まあ、雰囲気は出た、というところ。いいのかそれで。