だらだらとピーク検出続けてます。前回は信号処理のプロは「1行でピーク検出」書けると感動。素人のお惚け老人には思いつきませぬ。今回はツボにハマるとScilab関数で一撃でピーク位置を検出できるの件です。ツボは伝達関数から周波数応答を求めよう、なんて時です。ScilabのExampleをなぞってみただけだけれど一撃。お楽。
※「手習ひデジタル信号処理」投稿順 Indexはこちら
※Windows11上のScilab6.1.1およびScilab上のツールボックスを使用させていただいております。
今回実習してみた関数はfreson()
以下がScilabのHelpページ(日本語)です。
fresonは、「syslin関数で定義した」線形システムを入力にとって、ピーク周波数のベクトルを返してくれる関数です。一番簡単なところでは、
-
- 伝達関数(SISOシステムってこってすかい)を与えて、周波数応答を求める
なんてときに威力を発揮するであろう関数です。伝達関数が定義してあるのであれば、即ピーク位置を決定できますです。
Exampleに沿って実習
今回は上記のHelpページに掲載されていた実施例?にそって実行してみてます。まずは伝達関数の定義です。
上記では、よくやる文字「s」をラプラス演算子として使えるようにする「おまじない」はせず、ラプラス演算子として元々定義されている %s を素直に使って伝達関数を定義してます。なお syslinの第一引数に ‘d’ を与えると離散時間で定義できるのですが、上記では連続時間で定義してます。定義した結果の伝達関数が上記の h= のところに見えてます。
上で一端「連続時間」で定義した伝達関数(線形システム)を離散時間システムに変換するのが以下のdscr()関数です。このとき、サンプリング周期を第2引数で与えているのがミソです。このケースでは0.05秒、20Hzです(ということはナイキスト周波数は10Hzってことかい。)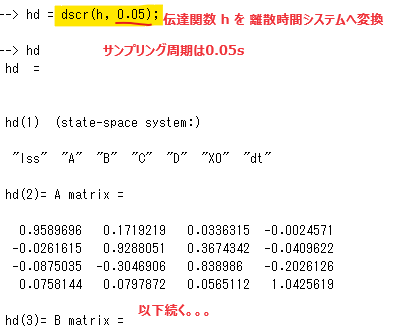
上記の後もだらだらと線形システムの定義が表示されるのですが、末尾のdtのところにサンプリング周期がしっかり記録されとりました。
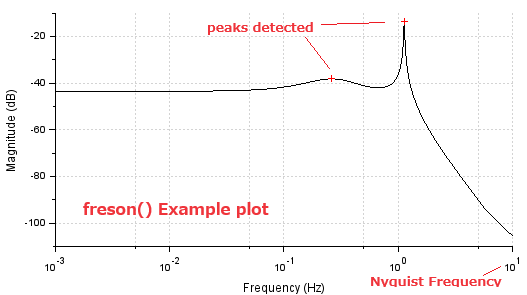
上記の黄のマーカ部分のように警告がでます。読んだ通りで計算時にナイキスト周波数(ここでは10Hz)を超える周波数が出てきたので無視したってことみたいです。描かれたボード線図が以下に。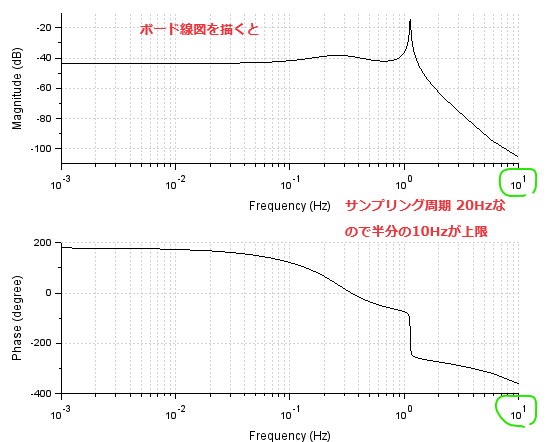
ナイキスト周波数を上限とするボード線図が描かれました。なお「連続な」伝達関数からボード線図を描いてもらった場合、もっと上の周波数まで勝手に描いてくれました(デフォルトはどこまで?)
離散でも連続でもほぼほぼ同じ(微妙に数字の下の方は異なる)結果が得られました。
上記で求まったのはピークの周波数位置(Hz)だったので、ボード線図上にお印をつけるためにはその時の「振幅」を求めておかねばなりませぬ。その処理が以下に。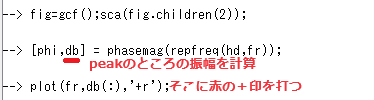
確かにピーク位置にお印ついとるな~。