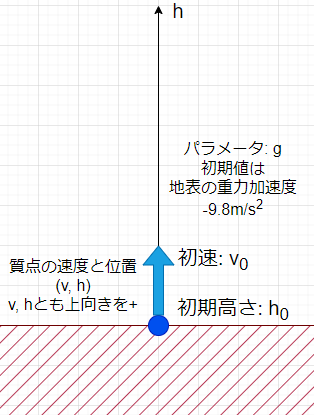
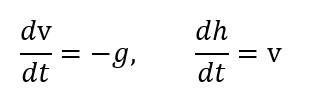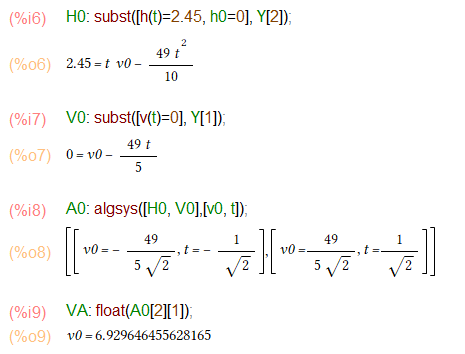今回はplotdf関数に戻って「実例」を描いてみたいと思います。「何の変哲もない」自由落下のモデルです。高さ方向のみ１次元、重力加速度は地表面の値で固定、空気抵抗なし、これ以上シンプルにできない？モデルです。ただし、重力加速度のみパラメータ化したので地表面だけでなく月面や火星面などいろいろ計算可能。よくあるやつね。
※「忘却の微分方程式」投稿順 index はこちら
※ MaximaおよびそのGUIであるwx Maximaの以下バージョンを使用させていただいております。
-
- Maxima 5.46.0(x86_64-w64-mingw32)
- wxMaxima 22.04.0
plotdf関数に与える微分方程式
１次元の高さhを上方向（重力方向と反対方向）にとり、一次元の速度vもhと同じ方向にとってます。初期値はh0とv0とします。重力加速度（定数パラメータ）はgです。
まずはplotdf関数に与える微分方程式が以下に。
この上なくシンプルですな。
plotdf関数には、微分方程式の形のまま与えればグラフをかけるのですが、念のため上記の微分方程式を解いておきます（といって、解くのはMaxima様ですが。）
何も設定しないと、浮動小数点数も分数化してくれるところがMaxima様です。
v(t)、h(t)を求めておいて何をしたいのかというと
人類が上方に飛び上がれる最高速度 v0
の「目安」を求めておこうと思うのです。どこぞで走高跳の世界記録2.45mというのを見たので、その高さから最速のv0を求めておこうと。実際には人間の重心は地表より高いところにあって個人ごとに異なるし、また複雑な形状の人体が高跳びのバーを越える挙動は１点で代表させるような数字でもないと思うのです。コマケー話を全部踏みつぶし、地表においた質点をどれだけの速さで上方に打ちだしたら2.45m高さに達するかの計算。
ということで、最速約6.93m/s という値が求まりました（これまた計算したのはMaxima様ですが。）
なお、遅れましたが plotdf関数の解説ページは以下に。
https://maths.cnam.fr/Membres/wilk/MathMax/help/Maxima/maxima_68.html
plotdfでグラフを描く
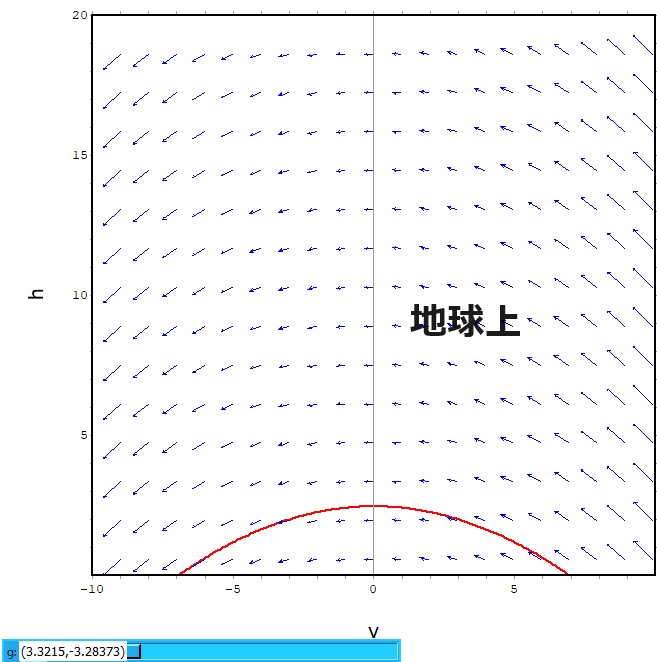
plotdfに与えた引数が以下に。微分方程式はシンプルですが、上記の初期値なども盛り込んだので、結構メンドくなってます。
load("plotdf");
plotdf([-g, v],
[v, h],
[parameters,"g=9.8"],
[nsteps, 1000],
[sliders,"g=0.1:50"],
[trajectory_at,6.93,0],
[v, -10, 10],[h, 0, 20])$
上記で描いたグラフが以下に。
このhv空間の中のテキトーな１点をクリックすれば、その点をh0, v0とした解が得られるのは以前にやった通りです。
上記のグラフが妙に上方向に空虚なのは、月面上で同じ初速の場合と比べたいからに他なりません。ちなみに月面での重力加速度は 1.62m/s2 だそうです。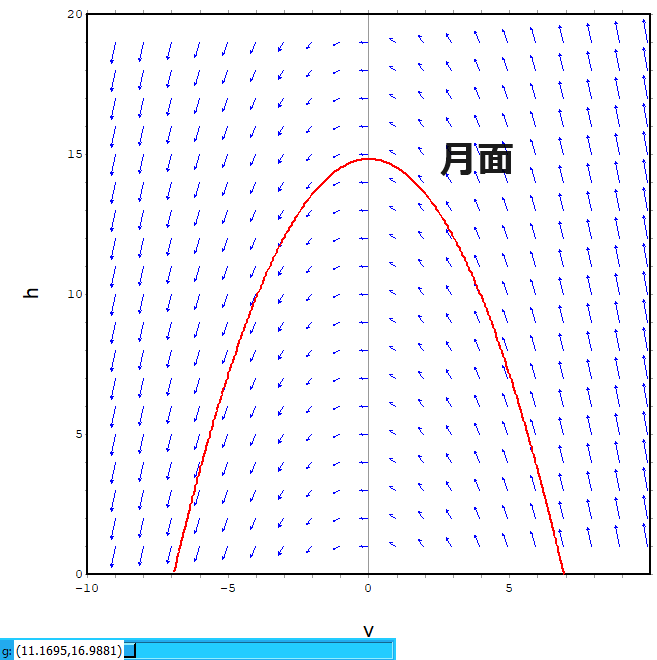
高くまで飛べるね。まあ、宇宙服着てそんなに飛ぶ人はいないと思うケド。
時間グラフ
plotdfは、上の「h、v空間」のような微分方程式の境界条件の空間のようなところでその解を調べるのに適しますが、時間グラフも描く機能がついてます。地表面でのグラフのときの時間グラフが以下に。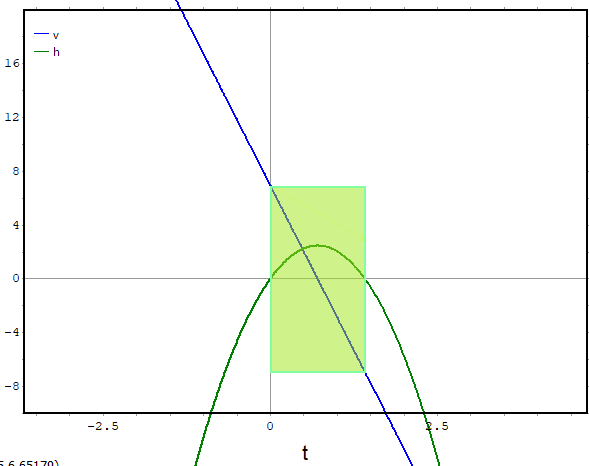
テキトーに広い範囲をプロットしてくれるので、上記には意味をなさないh < 0や t < 0の領域もプロットされてます。意味があるのは黄緑で色をつけたエリアですな。青の速度vは＋から‐へ単調に減少。緑の高さhは中央で最高値 2.45m（世界記録）をつける２次関数だ、と。
シンプルなやつはできるの当然。も少しこみいったらどうよ。