前回までにひととおりのパレットを舐めた（まだ残っているものがあるケド）ので、今回からはXcosを「実際の」問題（極めて単純化しているケド）に適用していきたいと思います。Maximaを使っている別シリーズでちょうど「月面上の垂直ジャンプ」を計算していたので、今回はそれと同じことをXcosでやってみます。
※「ブロックを積みながら」投稿順 index はこちら
※動作確認にはWindows 11の パソコン(64bit)上にインストールしたScilabの以下バージョンを使用しています。
Scilab 2024.0.0
別件シリーズ記事
人気の数式処理ソフトウエア（もちフリー）のMaxima様を使って、月面での垂直ジャンプの様子を計算しているのが、以下の別件記事です。
忘却の微分方程式(154) Maxima、｛plotdf}、「自由落下空間」、地球と月
Maxima様は数式処理ソフトなので、微分方程式を与えれば一撃で（解ける形ならばね。。。）一般解だろうが、境界値問題だろうが解けてしまいます。数値的に解くとか、具体的な数値を反映したグラフを描くなどは、余技といえるかもしれまへん。
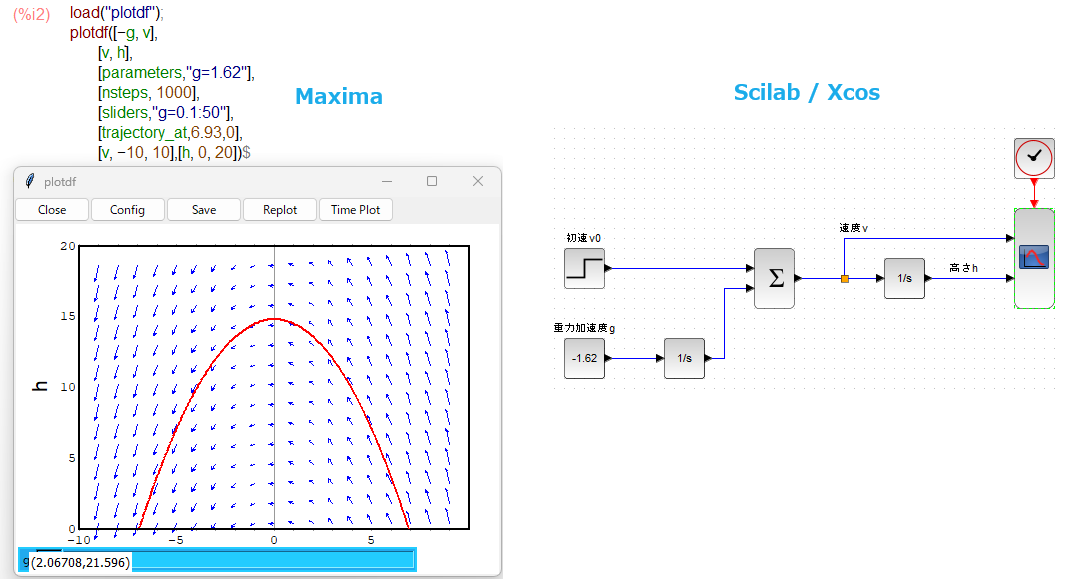
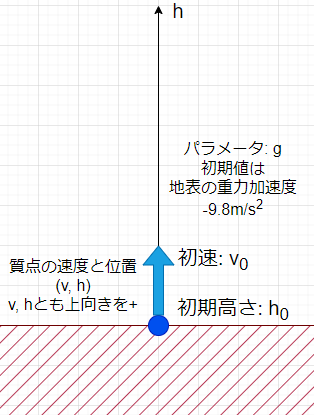
上記記事では、一定の重力加速度が働いている「空間」、空気抵抗などなし、について地表（月面）から垂直ジャンプしたときの速度vと高さhのなす「空間」に解をプロットしてみてます。単純化したモデルは以下の通り。
Xcosでの計算
忘却力の年寄は忘れてましたが、以前に本シリーズでも自由落下やってました。
ブロックを積みながら(138) Scilab/XCOSの配線？クセが強いのう。
上記では、Xcosのままならない配線に七転八倒する「ついでに」地表を離れること634m、東京スカイツリーの先端からの落下、という想定でグラフを描いてました。634mでも重力加速度は同じ、また、空気抵抗なしのやはり簡略版。
今回は地表（月面）からの垂直飛びなのでXcosモデルは以下のようにしてみました。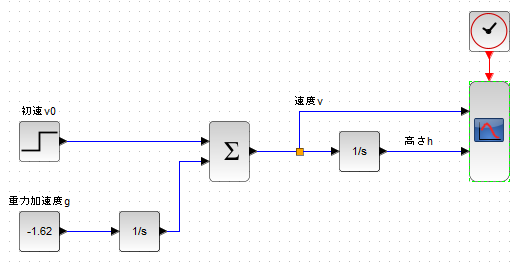
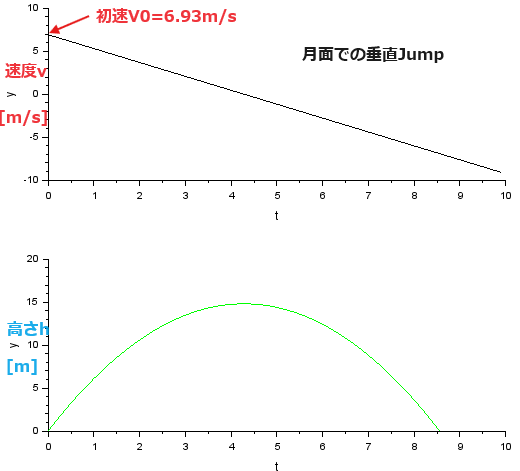
初速v0のステップ関数のところに、垂直飛びの上方向初速を与えます。今回与えたのは 6.93m/sという値です。別シリーズ回で、走り高跳びの世界記録高さから「推定」したインチキな値です。まあ、多分、現生人類的に達成しうる上限は抑えている値でないかと。
重力加速度gのところには-1.62m/sと指定してあります。上向き＋にとってあるので、下向きなのでマイナスです。1.62は月面での月の重力による値。
そして上記のモデルは以下の微分方程式表現と等価ってことであります。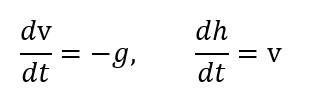
Xcosモデルだと、「1/s」なる積分ブロックで積分しとります。
モデルに描かせた結果が以下に。
横軸tの単位は秒です。
見たところ、Maxima様での結果と一致しているようだね。あたりまえか。次回からはMaxima様に頼らず、独自の道を探るっと。