今回、dynamicsパッケージの chaosgame関数を演習するのですが、本件、山嵜大輝先生著の同名の漫画とは「多分直接の」関係ありません。もしかすると漫画の方でもカオスからフラクタル図形を紡ぎだしているのかも知れませんが、読んでないので分かりませぬ。もしかすると奥底では結びついているのか?知らんけど。
※「忘却の微分方程式」投稿順 index はこちら
※ MaximaおよびそのGUIであるwxMaximaの以下バージョンを使用させていただいております。
-
- Maxima 5.46.0(x86_64-w64-mingw32)
- wxMaxima 22.04.0
chaosgame関数
前回、風神雷神のごとくマンデルブロ集合とジュリア集合に取り巻かれている?らしいThe dynamics packageが、恐ろし気な「複素力学系」へ誘っておるのに気づきました。Maxima様の The dynamics packageのドキュメント(日本語)は以下です。
上記のドキュメントの冒頭に登場するのが、chaosgame関数です。ただし、その「実施例」の描画図形を見るに
シェルピンスキーのガスケット
といわれる超有名な図形じゃないでしょうか?ここで、フラクタル素人老人は、つい「カオスゲーム」で検索してしまったわけです。そして山嵜大輝先生の同名の漫画の方に「誘われてしまった」というわけです。「誘われている」方向がちょっと違っている気がしたので気づきましたが。
さて、シェルピンスキーのガスケットについては別シリーズで中途になっていた「課題」の一つでもあったのです。別シリーズの過去記事が以下に
RustにいればRustに従え(8) シェルピンスキーのギャスケット、裏Pascal三角形
上記はRust言語を使って、「Pascalの三角形の計算結果の偶奇を判定する」という方法でシェルピンスキーのガスケットの「近似」図形を描いております。Pascalの三角形は順列・組み合わせを勉強している中学生(小学生?)が皆大好きでないかと思われる数字のピラミッド状のあれです。ただ、上記の過去記事では、i32型ではまったく不足。i64型(64ビット幅の符号付き整数)を駆使してようやく64段分のシェルピンスキーのギャスケット(近似)を描いてました。そしてi64型を単純に使った方法ではこれ以上は無理だと匙を投げてます。
Pascal恐るべし
というのが上記過去記事での結論?でした。無限に続くピラミッドを有限のビット長の整数では表現できへん、と。
しかし、ここに chaosgame関数が現れいでるのであります。以下『慶應義塾大学先端生命科学研究所』様の以下の論文ハイライトから1か所引用させていただきます。
Chaos Game Representationによるゲノムのフラクタル解析
一見不規則な変動(カオス)を元にしても,隠された法則性と十分な反復回数があれば,無作為な手順によってグラフを描くことでカオスアトラクターと呼ばれるフラクタル図形を得ることができる.
そうだったのね、それを体現しているのが chaosgame()関数らしいです。知らんけど。
それにchaosgame (Representation) はゲノムの塩基配列の解析にも使える?興味のある方は上記の文献へどうぞ。
というわけで、真正面からPascalの三角形を計算する方法でなく、カオスの側からシェルピンスキーのギャスケットのような図形を描く方法があったと。
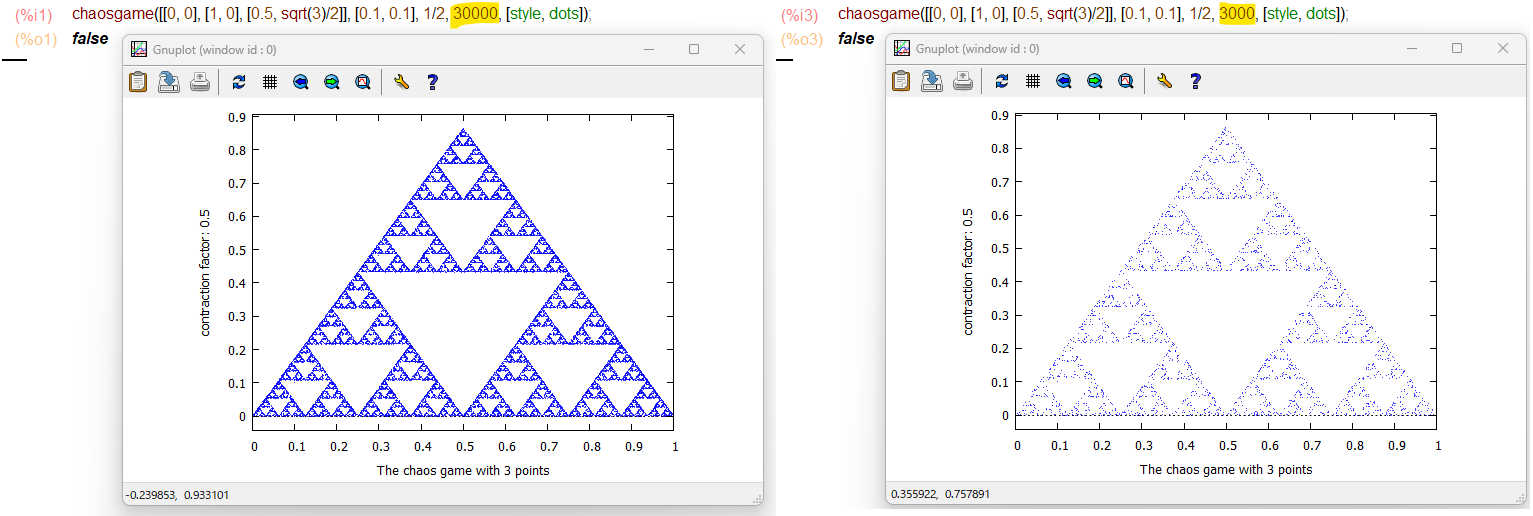
赤の部分で定義しているのは図形の頂点です。シェルピンスキーのギャスケットの場合は正三角とな。初期位置が微妙~なのは何か美しく描くためのノウハウなのかね? 1/2(あるいは0.5)はシェルピンスキーのギャスケットの場合、この値っす。
繰り返し回数30000回
実施例では繰り返し回数30000回のときの図形を描いてます。こんな感じ。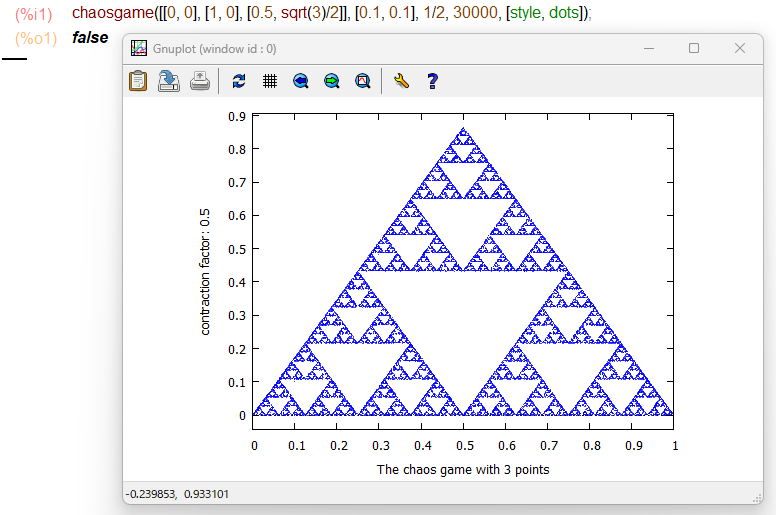
ただし、過去回の「端っこから正確に描く(でも無限階段を描かないとどこまでいっても近似)」という方法と比べると、今回の方は「全体(でも描いている途中のコマケ~ところは描きこめてない)をホンワカ」と描く方法っす。上記図形も拡大してみてみると、なにやら「まだまだ」な感じがしないでもないです。
繰り返し回数を増やしていけば(グラフィクスの解像度の範囲で)よりよくなる筈ですが、繰り返すのも芸がない?
繰り返し回数3000回
それではということで10分の1の繰り返し回数のところで打ち切った図形が以下に。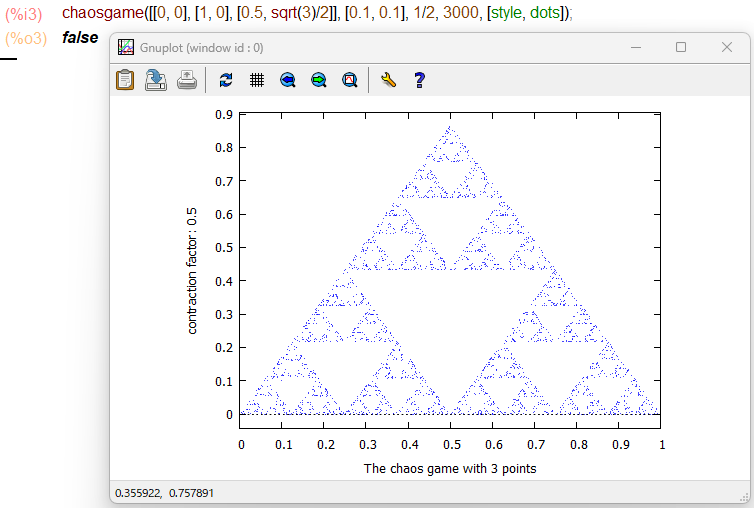
ぼんやりとシェルピンスキーのギャスケットが浮かび上がってきている雰囲気はあり。これがカオスゲーム関数の威力か?