前回は図形で描くカオスの中からフラクタルを紡ぎだすchaosgame関数でした。今回は「一次元離散力学系の族に関する軌道図」の中にトートツに出現するカオスを拡大したらばフラクタルなorbit関数です。お惚け老人はサッパリ分からんぜよ。まあ皆大好き(特に高校生?)漸化式を計算していたらいつの間にかカオスという感じです。
※「忘却の微分方程式」投稿順 index はこちら
※ MaximaおよびそのGUIであるwxMaximaの以下バージョンを使用させていただいております。
-
- Maxima 5.46.0(x86_64-w64-mingw32)
- wxMaxima 22.04.0
orbit関数
orbit関数の説明は以下のMaxima文書(日本語)の中に見つかります。
しかし、その説明を引用すれば以下のごとし。
パラメータ xを持つ一次元離散力学系の族に関する軌道図を描画します; この種の図は一次元離散系の分岐の研究に使われます。
素人老人にはサッパリです。orbit関数の引数を勝手に解釈するとこんな感じかと(上記の文書ではxと書かれているパラメータのところを勝手に μ で書き変えてます。)
orbits (F, y0, n1, n2, [μ, μ0, μf, μstep], options, …);
まず、Fに与える「数列」の定義ですが、ぶっちゃけ漸化式です。たとえば以下のような漸化式で数列を定義できる場合
x(n) = μ * x(n-1) * (x(n-1) – 1)
は、右辺を使って μ*x*(x-1) などと記述できます。知らんけど。
その数列の初期値が y0です。そして漸化式の計算を n1 回繰り返し(時間発展)た後、n1+1回目から n1+n2+1回目までのn2個の値をプロットします。ただしその際、パラメータ μ について μ0 から μfまで μstep毎変化させて計算を繰り返します。後はフツーにplot2dの描画オプション・パラメータを受け付けるみたいです。
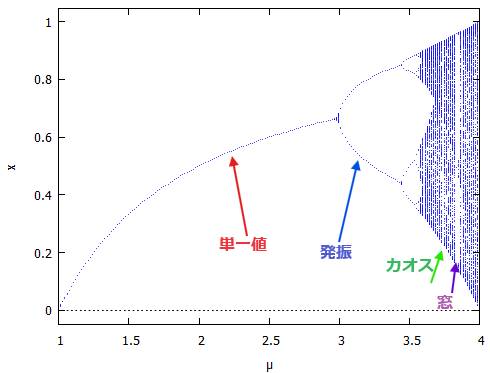
プロットは横軸にパラメータ μ をとり、縦軸に漸化式の値 x(n) をとる2次元のグラフです。あれまこんな感じ。
上記をみるとμ=1から3近くまでは、単一の値に「収束」してしまうみたい。それが3近くからは2つの値の間で「振動」し、さらにμが大きくなると「カオス」な事態に陥ると。ところが、カオスの中でも時折「窓」と呼ばれる限られた値の間を振動するモードが現れるっと。
上記で使った漸化式は、Logistic Functionであり、
X(n)=μ*X(n-1)*(1-X(n-1))
「メイの漸化式」とも呼ばれるみたいです。このことは『長嶋洋一』様の以下の文書に書かれてました。
上記の文書はもともとCQ出版 インタフェース誌1994年2月号の記事でハードウエア設計コンテストの課題のようです(30年前の御本ですがお惚け老人の本棚にあったです。当時の記憶はまったくないケド。)でも、まさに orbit関数で描きだせる「軌道」を扱ってます。pdf文書が上記から読め、その中にはCのソースも含まれてます。なお、上記のグラフを描く場合のorbit関数は以下のようになります。
orbits(μ*x*(1-x), 0.5, 100, 400, [μ, 1.0, 4.0], [style, dots]);
解説文書の例題
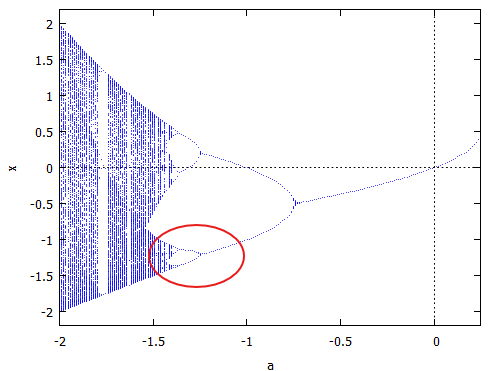
解説ページで扱われている漸化式Fの定義は x^2+a でした。それを描くのが以下に。
orbits(x^2+a, 0, 100, 400, [a, -2, 0.25], [style, dots]);
上記のグラフの赤丸付近を拡大する指定が以下に。
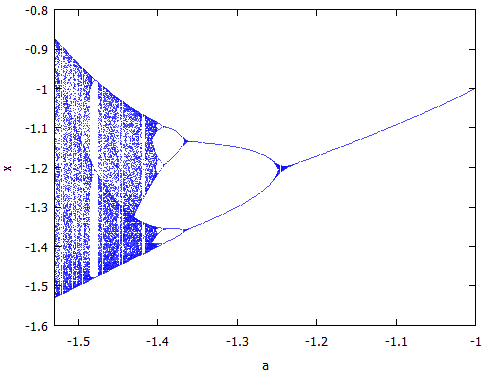
orbits(x^2+a, 0, 100, 400, [a,-1,-1.53], [x,-1.6,-0.8], [nticks, 400], [style,dots]);
拡大すると「またもや」な図形が見えてきます。フラクタルだあ~。