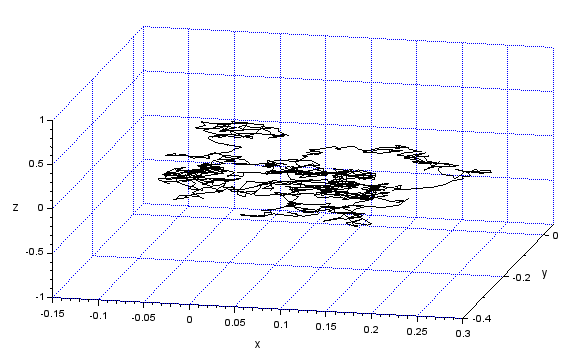
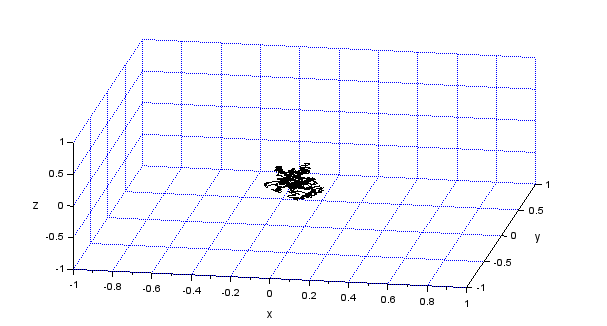
前回、3次元プロットに使えるブロック2種を練習。3次元空間に何やら「軌跡」を描ける気がしてきました。そこでお手軽に描けそうなものといって思いつくのがランダムウオーク、酔歩ってやつ。あっちによろよろ、こっちにぐたぐた、乱数使えば描けるハズ。何の工夫もなく3次元に拡張してプロットしてみるのみ。乱数の分布くらい変えてみるか。
※「ブロックを積みながら」投稿順 index はこちら
※動作確認にはWindows 11の パソコン(64bit)上にインストールしたScilabの以下バージョンを使用しています。
Scilab 2024.0.0
乱数ジェネレータ
以下の過去回にて乱数生成ブロック RAND_m は練習済です。
ブロックを積みながら(140) Scilab/Xcosの信号源その2。指示待ち?な奴ら
しかし真面目に練習していなかったので、復習デス。まずこのブロックですが、実数の乱数以外に複素数の乱数も発生可能です。まあ今回は実数のみです。さらに乱数の分布を以下から flag にあたえる値で選べるようになってます。
-
- 一様分布(Uniform distribution)、flag=0
- 正規分布(Normal distribution)、flag=1
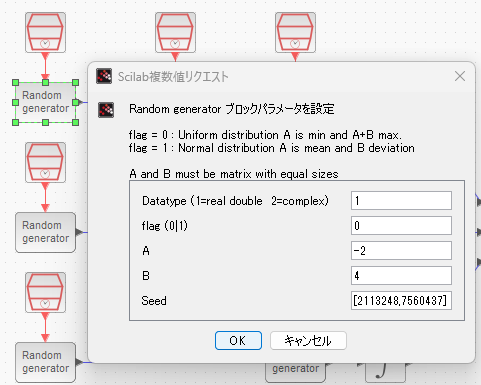
パラメータA、Bというものがあり、正規分布を選択した場合はAが分布の平均値で、Bが偏差となります。一様分布の場合はちょいクセ強です。Aが下限、A+Bが上限です。なお、乱数シードを与えるタイプ(シードは複素数!)です。
今回実験のフロー
今回実験のフローが以下です。4個のフロー並列です。いずれも3次元x、y、zでプロットしてます。左上は正規分布、左下は一様分布、右上は正規分布の乱数を「積分」するもの。右下は一様分布乱数を「積分」するもの。
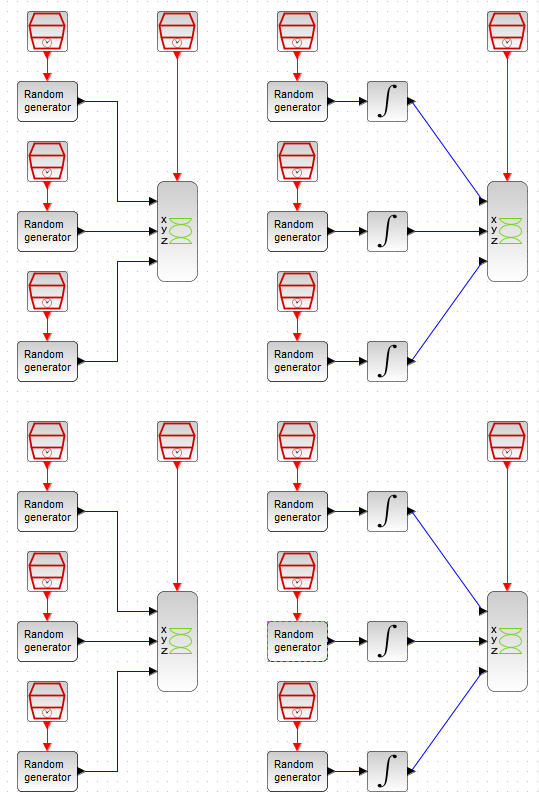
左側の結果をみれば、1回1回の乱数「振り出し」の結果を観察でき、右側の結果をみれば、酔歩的挙動が観察できるハズ。
正規分布の設定例(シードはブロックによって異なる)が以下に。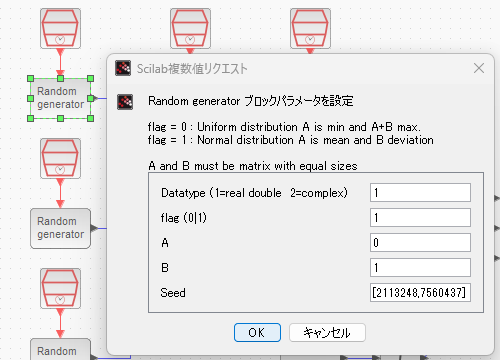
一様分布の設定例(シードはブロックによって異なる)が以下に。
 シミュレーション結果
シミュレーション結果
まず「素の乱数」を3次元にプロットしたもの。最初は正規分布。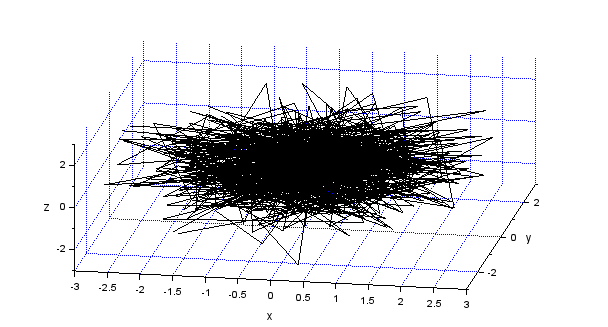
正規分布は裾野の限界があるわけではないので、ホンワカした塊にみえるような。お次は一様分布。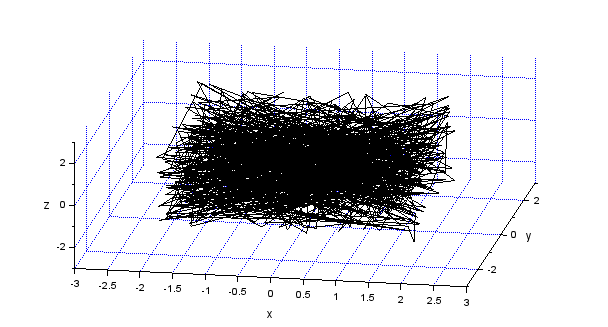
一様分布は、X、Y、Zのそれぞれで限界切っているので四角い箱の中に詰まっている感じになりますな。当たり前か。
さて、上記の「素の乱数」を積分したものが以下に。最初は正規分布。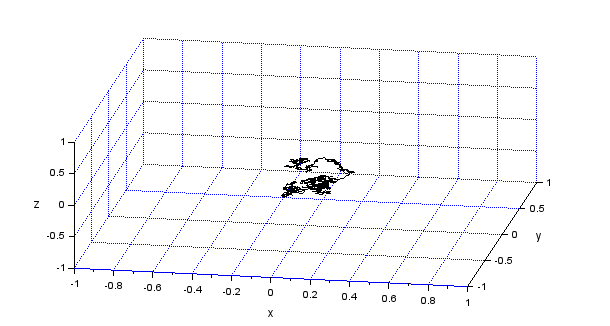
積分すれば、設定した平均値(今回は0)に近い値が予想されますが、そこになにやら軌跡が描かれるっと。これも酔歩と呼んでよいのかな?
これまたぐちゅぐちゅと動き回っておりますが、中央密集型?