前回は3次元空間に「酔歩」的ランダムウオーク軌跡を描きました。しかし3次元空間であるならばもっと描きたいものがあるのです。毎日のオオタニさんのご活躍で聞く、「打球速度180km/h、打球角度30度」といった打球の軌跡ですね。何度か自由落下の計算はしているのですが、3次元になったのでやり直すのもいいかと。
※「ブロックを積みながら」投稿順 index はこちら
※動作確認にはWindows 11の パソコン(64bit)上にインストールしたScilabの以下バージョンを使用しています。
Scilab 2024.0.0
第163回で「月面での自由落下」計算しております。「月面」ということは空気抵抗その他、流体力学的もろもろの効果は無。単純な落下ということです。ただし今回は地球表面、3次元空間を想定。
打球速度と角度
毎朝のニュース等で目にするのは「打球速度 180km/h、打球角度30度」といった表現です。速度は初速ということで良いでしょうか。キロメートル毎時表現です。また角度は水平方向を0度として「仰角」を表現しているみたいです。
一方、物理では速度は m/s 単位がフツー。また角度は弧度法にてラジアン表示っす。また極座標表示をする場合、天頂方向を0として水平方向を π/2 とするのが一般的かと。
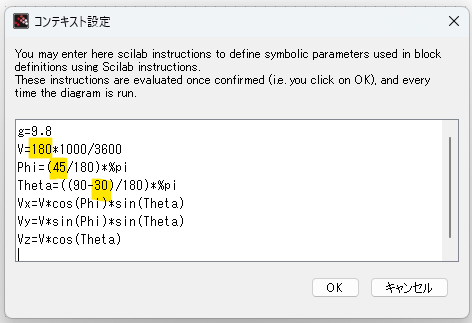
そこで打球速度と仰角についてはニュースで記載されている表現通り入力し、Xcosのコンテキスト設定内で「物理的」にフツーな単位、座標系に換算して計算することといたしました。原点をホームベースに置き、以下のような座標系です。
-
- X軸、1塁線方向 m 表示
- Y軸、3塁線方向 m 表示
- Z軸、天頂方向 m 表示
黄色のマーカーつけたところ
-
- 180は、打球速度の180km/hのつもり
- 45は、水平方向角度φ、X軸とY軸の中間、ちょうどセンター方向
- 30は、垂直方向の仰角、θは天頂0とした弧度法角度に換算
であります。ここを変更すれば「各種打球」を味わえるはず(空気抵抗ないけど。)
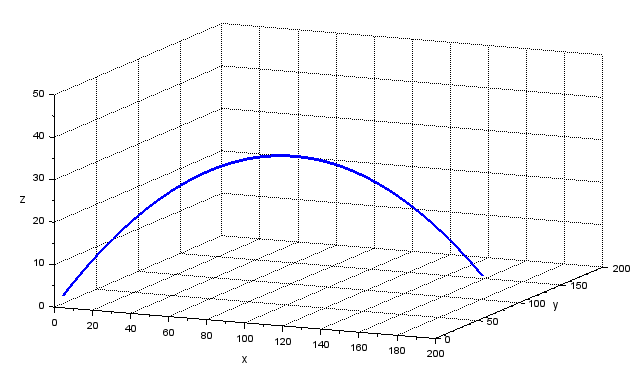
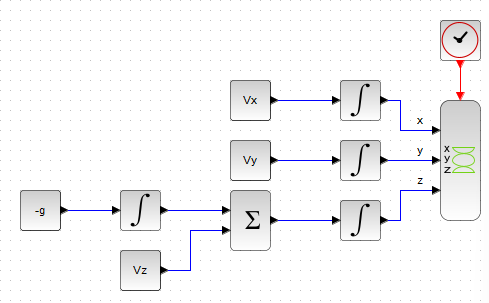
今回実験のフローとそのシミュレーション結果
方向毎の初速成分は上記のコンテキスト設定で計算済なので、X方向、Y方向は積分すれば打球位置が計算できます。Z方向だけは、地球重力gのマイナスを積分して初速に加えて速さを計算してます。後は3次元プロットするだけ。
結果はこんな感じ。
両翼200mの空間の中の軌跡(空気抵抗ないから飛びすぎ)ですな。3次元っぽい軌跡が描けたのでいいか。