
前回は離散コサイン変換でした。今回は距離変換です。2値画像の各画素から最も近い画素値「0」(通例、黒にみえるハズ)までの距離を計算し、(2値でない)距離値がつまった配列(距離マップ)を返してくれるもの。使い途は御随意。なにかの処理の下ごしらえ用かね?でも「距離」といって距離の計算の仕方にはいろいろあるのだと。
※「手習ひデジタル信号処理」投稿順 Indexはこちら
※Windows11上の Scilab2024.0.0およびScilab上のScilab IPCVツールボックスを使用させていただいております。
Distance Transform
距離変換は、上で述べたとおりの単純な変換っす。でも距離をどうやって計算するの、というところにScilabのimdistansf関数は3通りの選択を用意してくれてます。
-
- マンハッタン距離、シティブロック距離 L1ノルム
- ユークリッド距離、L2ノルム
- チェビシェフ距離、チェス盤距離 L∞ノルム 最大値ノルム
代表的なお名前ということで距離の定義のお名前を書き、その横に別名を列挙させていただきました(123は関数の引数そのもの。お名前の並び順は老人の思いつきデス。)いろいろあるのね、距離。調べてみると、距離には実は「もっともっと」いろいろな距離があって忘却力の素人老人を深みへと誘ってくれるのです。まあ今回対象関数は上記の3つだけなので、まあいいか。
距離を測る2点の座標を(x1, y1)、(x2, y2)とすると上記の1,2,3の定義は以下のようです。明快?
-
- |x1-x2| + |y1-y2|
- sqrt(|x1-x2|2 + |y1-y2|2)
- max(|x1-x2|, |y1-y2|)
処理例
helpの処理例を変形し、全3種類の距離計算法をすべて適用してみたものが以下に。
S = imread(fullpath(getIPCVpath() + "/images/three_objects.png"));
Sgray = rgb2gray(S);
Sb = im2bw(Sgray,0.1);
S1 = imdistransf(Sb, 1);
S2 = imdistransf(Sb, 2);
S3 = imdistransf(Sb, 3);
subplot(151); title('Original'); imshow(S);
subplot(152); title('BW'); imshow(Sb);
subplot(153); title('Manhattan'); imshow(S1);
subplot(154); title('Euclidean'); imshow(S2);
subplot(155); title('Chebyshev'); imshow(S3);
その結果が以下に。
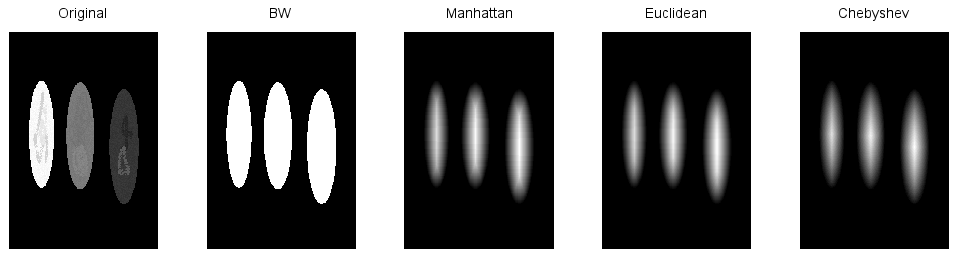 3通りの距離計算してみたけど、結果はほとんど見分けがつかんです。ビミョ~。
3通りの距離計算してみたけど、結果はほとんど見分けがつかんです。ビミョ~。
念のため、S1からS3の配列の平均値をとって比べてみましたぞ。
微妙だけれども確かに差はあるようです。画像処理のプロはこの辺のコマケーところでいろいろ出し入れしているのか?知らんけど。