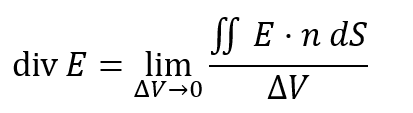前回は、スカラー場からベクトル(勾配)を求めるグラディエント(grad)を計算してみました。プロットもなんとかなる感じ?今回はベクトル場から発散(ダイバージェンス)を求めるdiv()関数を試用してみます。こんこんとベクトルが湧いてくるのよ?でも、お惚け老人には3次元空間ベクトル場の表現はムツカシイのでいつもの2次元ね。
※「忘却の微分方程式」投稿順 index はこちら
※ MaximaおよびそのGUIであるwxMaximaの以下バージョンを使用させていただいております。
-
- wxMaxima 22.04.0
- Maxima 5.46.0(x86_64-w64-mingw32)
- SBCL 2.2.2 (SBCL = Steel Bank Common Lisp )
毎度のvect パッケージと plotdf パッケージ
ベクトル解析の関数どもを計算するのに vect パッケージを、またベクトル場をプロットするのに plotdf パッケージを使わせていただいております。まいどですが、vect パッケージのマニュアルページが以下に
23. Matrices and Linear Algebra
plotdf パッケージが以下に。
https://maths.cnam.fr/Membres/wilk/MathMax/help/Maxima/maxima_68.html
divergence
遥かな古代、大学の初年級だったと思うのですが、電磁気学の講義の最初の方で、
発散とは、ある点の近傍についての単位体積あたりの力線の出発数である
とか習ったような、習わんかったような。。。
爾来、膨大な時間があったものの、まったく進歩していない年寄デス。上記の式で、ΔVという体積が出てきておるので、本来3次元空間の中で計算すべきダイバージェンスなのでありますが、例によって3次元空間のプロットがお惚け老人にはムズカシーという理由で次元を落として2次元空間で計算することも可能。
2次元空間でのダイバージェンスを、2次元の∇演算子と内積・を使って書き表すとこんな感じ。
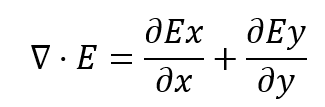 そして、vectパッケージには2次元でも3次元でも(切替はdimension制御変数への代入による)計算できる div()関数が備わってます。
そして、vectパッケージには2次元でも3次元でも(切替はdimension制御変数への代入による)計算できる div()関数が備わってます。
先ずはベタなベクトル場の例
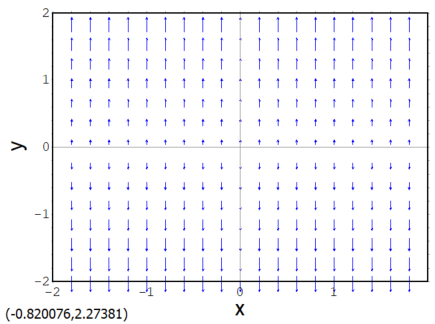
まずは「のっぺりした」ベクトル場 E1 です。x座標にはよらず、y座標に比例した「何か」がy成分を決めるもの。
load ("plotdf");
E1 : [0, y];
plotdf(E1, [x, -2, 2], [y, -2, 2]);
上記のベクトル場に対してダイバージェンスを計算し、プロットしてみるコードが以下に。dimension:2ということで2次元を指定してます。
load ("vect");
dimension : 2;
D1: ev(express(div( E1 )), diff);
plot3d(D1, [x, -2, 2], [y, -2, 2],
[grid, 39, 39],
[palette, [gradient, red, orange, yellow, green]],
color_bar, [xtics, 1], [ytics, 1], [ztics, 4],
[color_bar_tics, 4])$
結果はのっぺりした「定数1」なので、ちょっとつまりませぬ。全面的に1が湧き出しているってか?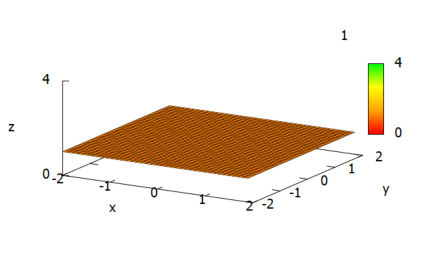
続いて人工的な例
もうちょっと凸凹のあるグラフが得たいということでアーティフィシャルなベクトル場E2を定義。
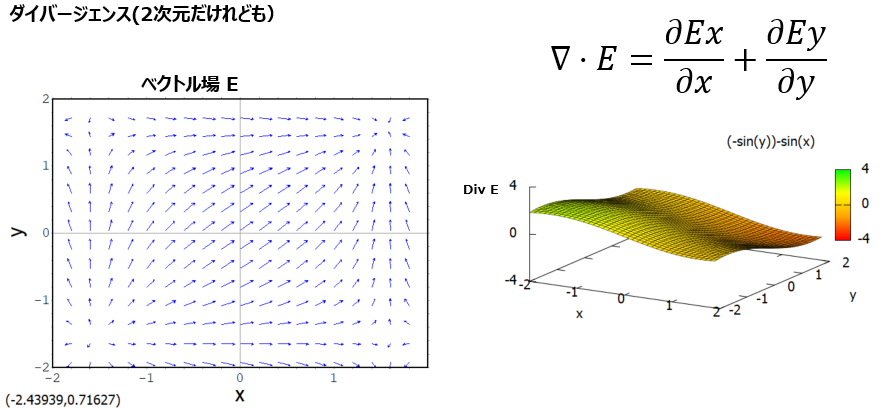
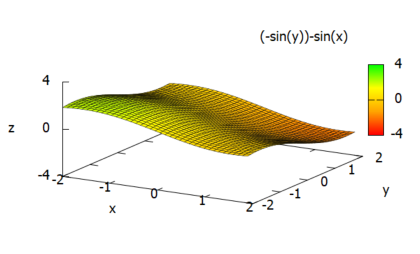
E2 : [cos(x), cos(y)]; plotdf(E2, [x, -2, 2], [y, -2, 2]);
ベクトル場のプロットが以下に。左下の方で「湧き出し」て右上の方で「吸い込まれ」ている気がしないでもない。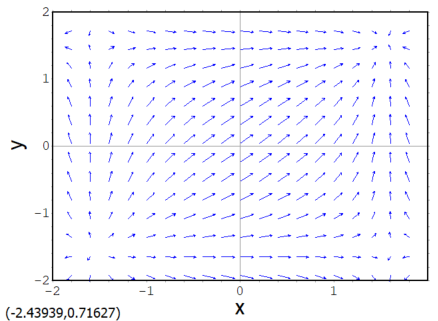
そして上記のベクトル場のダイバージェンス(div)をとると、
D2: ev(express(div( E2 )), diff); plot3d(D2, [x, -2, 2], [y, -2, 2], [grid, 39, 39], [palette, [gradient, red, orange, yellow, green]], color_bar, [xtics, 1], [ytics, 1], [ztics, 4], [color_bar_tics, 4])$
確かに左下の方で「湧き出し」て右上の方で「吸い込まれ」ているみたい。いいのかそんな感じで。