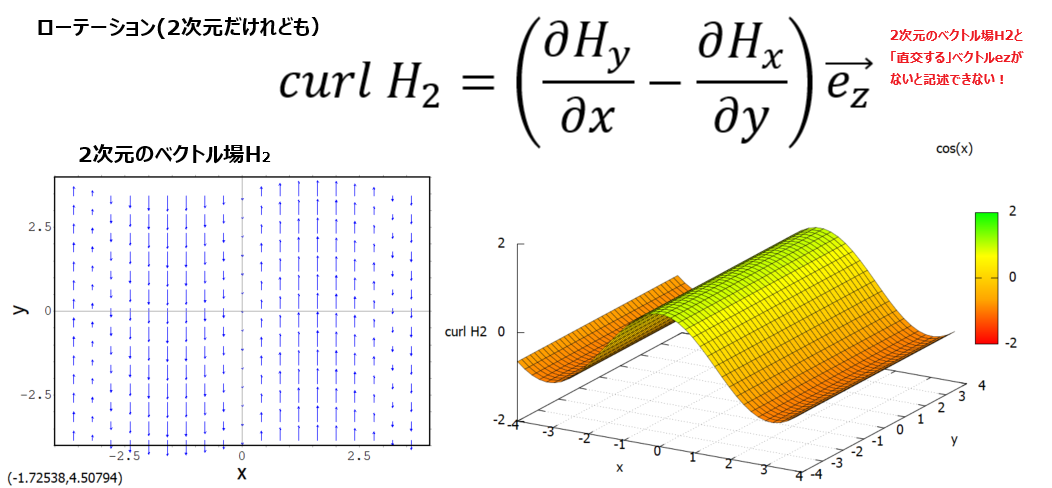
前回はダイバージェンス(div)、今回はローテーションです。遥かな太古、お惚け老人が学校でベクトル解析を習ったとき、rot (rotation)というお名前で習いました。rotでなく、curl とお書きになる流儀もあるみたい。Maxima様はどうも curl 流であるようです。rotと書いたらエラーになりましたぜ。
※「忘却の微分方程式」投稿順 index はこちら
※ MaximaおよびそのGUIであるwxMaximaの以下バージョンを使用させていただいております。
-
- wxMaxima 22.04.0
- Maxima 5.46.0(x86_64-w64-mingw32)
- SBCL 2.2.2 (SBCL = Steel Bank Common Lisp )
毎度のvect パッケージと plotdf パッケージ
毎度になりますが、お世話になるパッケージ共のマニュアルページへのリンクを貼らせていただきます。vectページ(日本語)が以下に
23. Matrices and Linear Algebra
plotdf パッケージ(英語)が以下に。
https://maths.cnam.fr/Membres/wilk/MathMax/help/Maxima/maxima_68.html
rot あるいは curl
さてね、rot あるいは curl ですが、ベクトル場を rot したら回転している面と直交する方向のベクトルが登場してしまいます。本来、3次元のベクトル空間をrotに捧げると3次元のベクトルが得られるべきでないかと。
しかし、お惚け老人にとっては、3次元空間を偏微分する様子とか、そこから得られた3次元のベクトルとかグラフにするのがいつもの通り難しいです。そこで rot あるいは curl についても、ターゲットとなるベクトル場H2はxy平面内の2次元としてしまいました。するとこんな感じ。
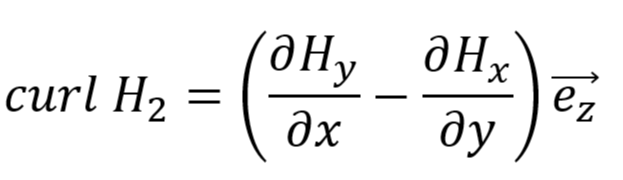
しかし、rot あるいは curlを作用させた結果はxy平面内にはおさまりきれませぬ。xy平面とは直交する単位ベクトル Ez なるものを考えて、上記のような形となります。まあ、この形だと2次元の平面に対して、Z方向に curl H2の値(スカラー的な大小)をプロットしてやれば図を描けます。ラッキー?違うか。
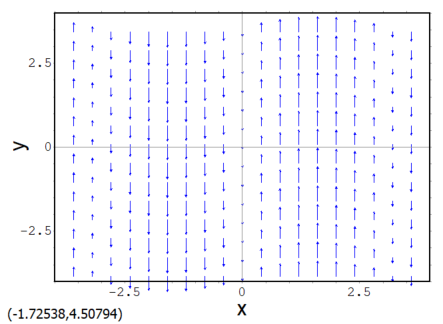
まずは2次元の平面内のベクトル場 H2
例によって plotdfパッケージを使ってH2を描いてみます。
load ("plotdf");
H2: [0, sin(x)];
plotdf(H2, [x, -4, 4], [y, -4, 4]);
単純な「場」ではあるけれど、x=0の付近に相反するベクトルから、反時計回りの小回転が多数できそうな気がしてきました。気のせいか?また、x=±π(3.14)付近には時計回りの渦が見えてきそじゃあ~りませんか。
2次元の rot あるいは curl を求めてみる
上記までくれば、再び vect パッケージにお出まし願って、以下のような計算で結果を図示することができまする。
load ("vect");
dimension : 2;
R2: ev(express(curl( H2 )), diff);
plot3d(R2, [x, -4, 4], [y, -4, 4],
[grid, 39, 39],
[palette, [gradient, red, orange, yellow, green]],
color_bar, [xtics, 1], [ytics, 1], [ztics, 2],
[color_bar_tics, 2], [zlabel, "curl(H2)"])$
curl H2の「大きさ」をXY平面と直交するZ軸に描いたものが以下に。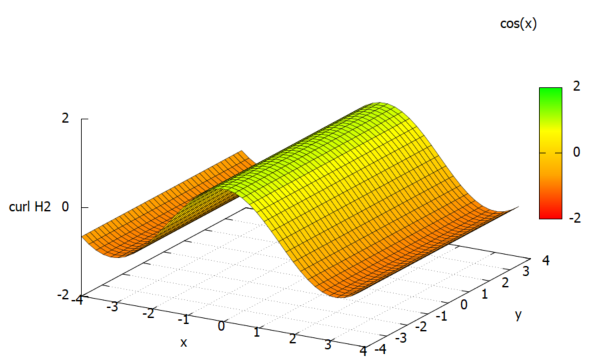
curl H2、計算できてるみたい。。。