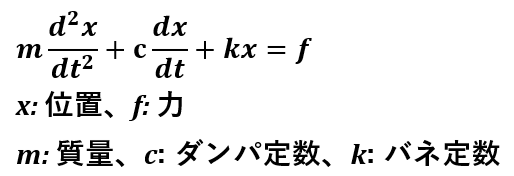別シリーズ「忘却の微分方程式第176回」にて、ラプラス変換関数を使って伝達関数を求めてみました。Maxima様にお願してメンドクセー「伝達関数」が得られるとなれば、ブロック線図を描くのはお茶の子サイサイ? あとはScilab/Xcos側に伝達関数を輸入すれば時間領域でのシミュレーションができるハズ。サンプルを実地検証。
※「ブロックを積みながら」投稿順 index はこちら
※動作確認にはWindows 11の パソコン(64bit)上にインストールしたScilabの以下バージョンを使用しています。
Scilab 2024.0.0
別シリーズの「例題」
みんな大好き Maxima は「フリーの数式処理」ソフトウエアの代表選手です。微分、積分、三角関数、代数方程式でも微分方程式でも「数式のまま(具体的な数値になってなくても)」解くことが可能。数学力のない忘却力の年寄りには必携のツールであります。別シリーズでは使い方をいろいろ修練。
今回は、そのMaxima様で微分方程式からラプラス変換して伝達関数に変換した結果を、Scilab / Xcos (Scicos) 上で受け止めて時間領域でシミュレーションをしたいと思います。
上記のアリガチな力学系(適当な定数を選んでやれば減衰振動するハズ)の微分方程式から、以下のようなブロックダイアグラムに書き込まれている伝達関数をもとめてます。
Scilab / Xcos上でのフロー
上記のようにブロックダイアグラムに書き込める伝達関数が求まっているのであれば、Xcosのフローは簡単。こんな感じ。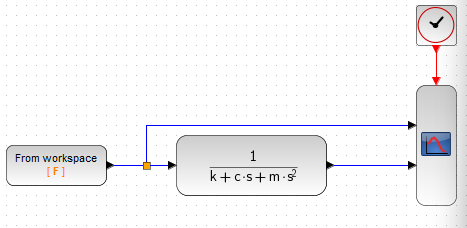
外部からの入力として力Fの波形をScilab上の変数として与えてみます。こんな感じ。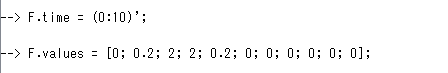
とりあえず時間は 秒 、力は N ということにしておきます。
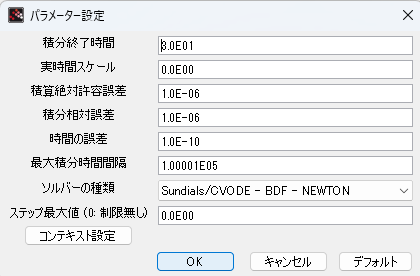
一方、伝達関数の中に現れる、質量、ダンパ定数、バネ定数などはコンテキスト設定で与えておきます。こんな感じ。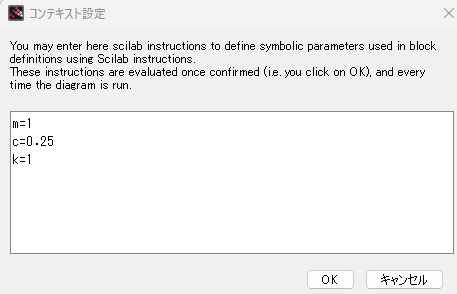
今回は、減衰振動を味わいたかったので30秒分です。
シミュレーション結果
Scilab / Xcos によるシミュレーション結果が以下に。上の「黒」グラフが入力である力F、下の「緑」グラフが出力である位置 X です。横軸は時間[秒」ね。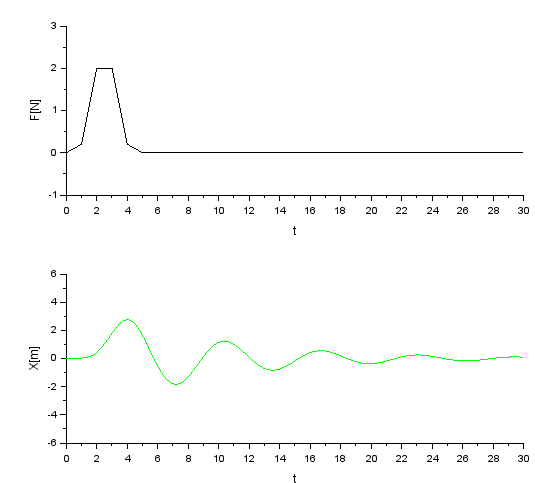
メンドイところはMaximaとScilab/Xcosにおまかせ。何も頭を使ってね~。