今回は２次元画像用の周波数ドメインでのフィルタを設計するときに「便利」らしい可視化ツールです。これが何故か充実。３種類もあります。素人老人はその理由を知らず。まあお好みで使えるっと。しかし実際の画像に周波数ドメインでのフィルタを適用してみないとその御利益が身に染みないのお。しかしそれは次回か。
※「手習ひデジタル信号処理」投稿順 Indexはこちら
※Windows11上の Scilab2024.0.0およびScilab上のScilab IPCVツールボックスを使用させていただいております。
Filter Design and Visualization
今回手習ひしてみるFilter Design and Visualizationのメインは、２次元の画像に適用できる「周波数ドメイン」フィルタを設計することにあるみたい。例えば高い周波数成分（ギザギザした奴らかも）などを落として低い周波数成分（ゆったりした大きな変化）を残すとか「周波数」（画像なのでピクセルの距離が離れていれば低いってことでいいかね）に応じた応答を得られるのかな。
フィルタの周波数応答可視化用ツール
さて、そんなフィルタを設計するときにフィルタ自体も可視化して吟味したいということがあるみたい。素人老人はイマイチどころか、なかなかついていけない世界っす。これも手習ひ。
ただしツールとしては単純です。突き詰めて言えば「二次元配列を3D画像として表示」するだけのもの。ツールは以下の３種類。
-
- imsurf
- imsumoothsurf
- immesh
surfという文字に一瞬SURFアルゴリズムかと思った老人は大間違いデス。多分surfaceのsurfね。
わけわかってない素人が、やりました感だすのは、実際に使ってみるのが一番。今回の処理例としてはこんな感じ。ガウシアンフィルタを何やら膨らかせた後、ビジュアライズしてるみたい。
f = fspecial('gaussian');
F = fftshift(fft2pad(f,256,256));
scf(0); clf;
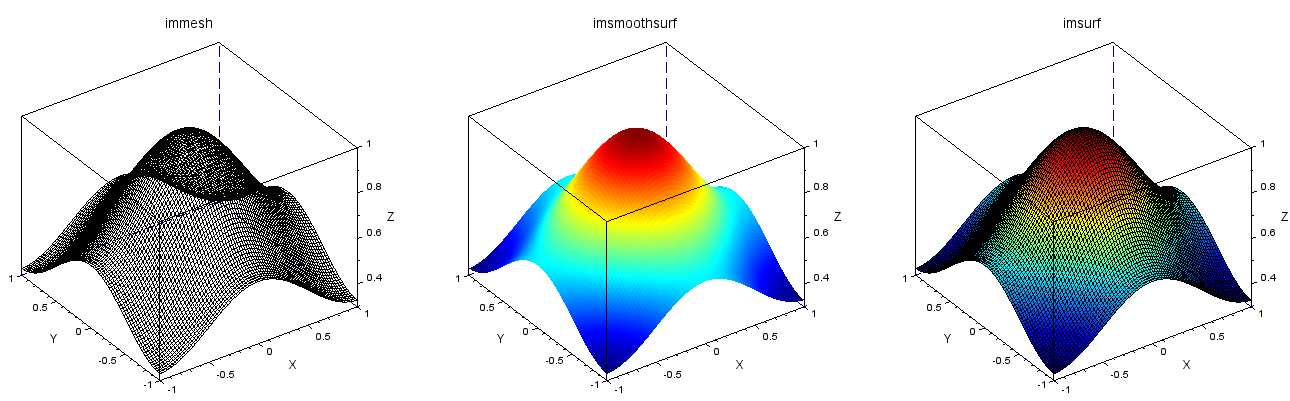
subplot(131); title('immesh'); immesh(abs(F),100);
subplot(132); title('imsmoothsurf'); imsmoothsurf(abs(F),100);
subplot(133); title('imsurf'); imsurf(abs(F),100);
そして上記の結果が以下に。
左端がmesh。白黒で地味ですがメッシュなので向こう側が透けて見えてます。一方右の２つがsurf。表面に隠された裏側は隠れてます。
まあね、数字の羅列を見るよりかは分かり易い？
処理ステップをステップ・バイ・ステップで確認
さて上記の処理例でさらっと通り過ぎてしまった処理例についてステップ・バイ・ステップで確認してみると
f = fspecial('gaussian');
ガウシアンフィルタ（画像に対するLPF的なもの）を作成してます。何も追加の指定していないので、フィルタのサイズは３ｘ３、σ=0.5のデフォルト値で生成されます。この時点でのfは３ｘ３の実数配列です。
２行目のfftshift()関数の中身が以下です。
fft2pad(f,256,256)
与えられたフィルタ(実数3×2) f を256×256サイズになるようにパディング（ゼロづめ？）した後、fft2（２次元の高速フーリエ変換関数）を使用して256×256サイズの複素行列に変換しているらしいです。ただこのままではFFTはかかった、というだけでフィルタの形ではないみたい。
上記の結果を以下のように fftshift 関数に通すことで
F = fftshift(fft2pad(f,256,256));
fft出力を再配置し、スペクトルの中心に周波数0を移動。これで複素フィルタの雰囲気例的なものができたのか？知らんけど。
後はプロットするときには、複素数なので忘れず abs()関数をとっておくっと。
途中経過のプロットが以下に。まずはオリジナルの３ｘ３ガウシアンフィルタ。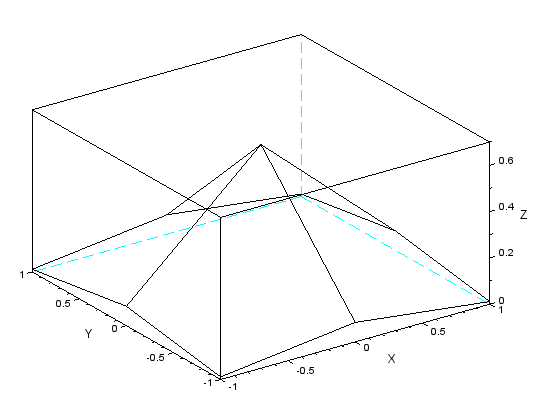
上記に対してfft2pad(f,256,256)してFFTかけた結果が以下に。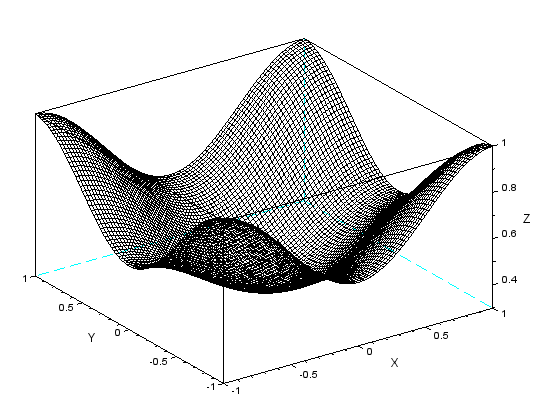
周波数０のところはコーナーにいるみたい。知らんけど。