信号処理素人老人が、Scilabの「信号処理のデモ」物色中。今回はみんな大好きConvolutionです。最近、コンボリューションというとニューラルネットでばかり遭遇するような気がします。気のせいか?まあ、フツーに信号処理でも大活躍ですな。今回はそんなコンボリューション関数の復習ということで。
※「手習ひデジタル信号処理」投稿順 Indexはこちら
※Windows11上の Scilab2024.0.0を使用させていただいております。(Scilabについては御本家 Scilab 様へ)
今回動かしてみるデモ
以下のScilabデモ選択ウインドウから「1次元畳み込み」を選択すると実行できるのが今回のデモです。
今回のデモは「グラフ1枚描いて終わり」のシンプルなものです。まあ走らせたグラフを見れば信号処理素人老人にもそこはかと内容の想像がつきますが、ソースを読んで内容を確認したいと思います。デモのソースファイルは「いつものところ」に格納されている以下です。
conv.dem.sce
「いつものところ」のパスは過去回に書いてありますが、走らせたグラフ・ウインドウのメニューバーに「-コードを表示ー」というメニューが現れるので、それを押した方が手っとリばやいっす(表示されるか否かはデモによるのでありますが。)デモの中身をザクッリ読むとこんな感じ。
-
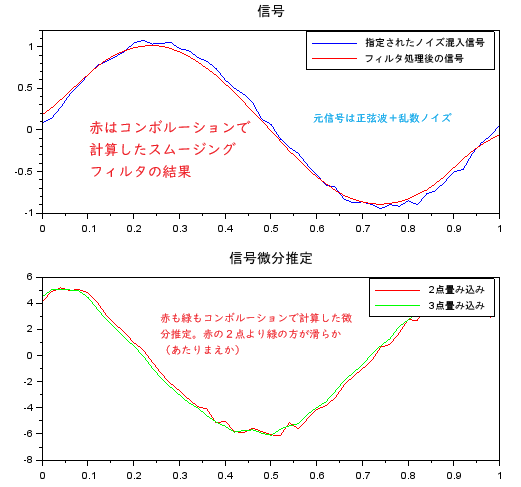
- ターゲットとなる元信号を正弦波+ランダムノイズということで生成
- 天下りのスムージングフィルタ定数ベクトル(8点の線形位相FIRローパス・フィルタ、数字をみるとほぼほぼ移動平均みたいなやつ)でコンボルーション処理して正弦波を推定。
- 元信号を2点および3点の「定数ベクトル」とコンボルーションして、信号微分推定(Signal derivative estimate)
いつものように、Googleの生成AI、Gemini 2.0 Flash様に解説願った冒頭のところが以下に。![]()
いつものように、わかったような、わからぬような。さてご回答の末尾をみやれば以下の如し。![]()
結局、フィルタを作るお前の自己責任じゃと。そういうこと?
なお、ソースコードをみると、conv()関数で離散一次元畳み込みの計算をしています。conv()関数は、計算のshapeとして以下の3通りのチョイスがあるので便利っす。
-
- “full” デフォルト、A、B全長に対する完全な畳み込み、Aより長い
- “same” 結果はAと同じ長さのベクトル
- “valid” 結果はAのゼロパディング無の畳み込み、Aより短い
ただし、過去回でも遭遇した朧気な記憶があるのですが、convol()関数を使った方が速い(演算並列化してくれているみたい)ので、巨大な計算にはconvol()の方がよさそうです。ただし、convol()には上のようなオプションはないようです。
デモの結果
conv()関数で計算する相手のベクトル次第で、ノイズを抑制して信号を推定したり、信号の微分を推定したりと、思うがままじゃと。コンボルーションすごい?あたりまえか。