「サイエンティフィックPythonのための」IDE、Spyder上にてScientific Python Lecturesの実習中。前回は必ず使うけれど覚えきれない小技でした。つづいて各種プロットの実習に入るのですが、Lecturesに含まれていないプロットを一つ見つけました。ヒストグラムです。気づいたので先に自習。
※「 ソフトな忘却力」投稿順 Index はこちら
※Scientific Python Lectures様のコースは例題だけでなく、エクササイズなども充実、それを全部順番に解いていったら必ずや立派な人になれるだろ~とは思います。でもキチンとやったら、死ぬまでに終わらない、と。今回は4.3以降に入る前に自主練習。
※お惚け老人に代わって Googleの生成AI、Gemini 2.5 Flash 様にご説明をいただいた部分があります。
ヒストグラム
たまたまレクチャーの4.4で落ちていたからといって何か特に意図があったとも思われません。ヒストグラムに関しては Numpy も Matplotlib も結構サポート充実していたりします(個人の感想です。)
Numpy側ではヒストグラム用の集計機能があります。
また、Matplotlibのヒストグラムのプロット機能の解説が以下に。
上記を読ませていただくと分かりますが、matplotlibとnumpyは裏で「握って」おり、Matplotlibのhist関数呼び出すと中でNumpyの集計機能を使ってくれることもあるみたい。
上記の解説を読みながら、Spyderのエディタ画面で書いたスクリプトが以下に。
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
"""
Created on Thu Jun 5 17:27:39 2025
@author: jhalfmoon
Histgram plot example
"""
import numpy as np
import matplotlib.pyplot as plt
dat = np.random.rand(10000, 1)
datHist, datEdges = np.histogram(dat, bins=19)
# %%
plt.figure(1)
plt.stairs(datHist, datEdges)
plt.title("Stairs")
plt.show()
# %%
plt.figure(2)
plt.hist(datEdges[:-1], datEdges, weights=datHist)
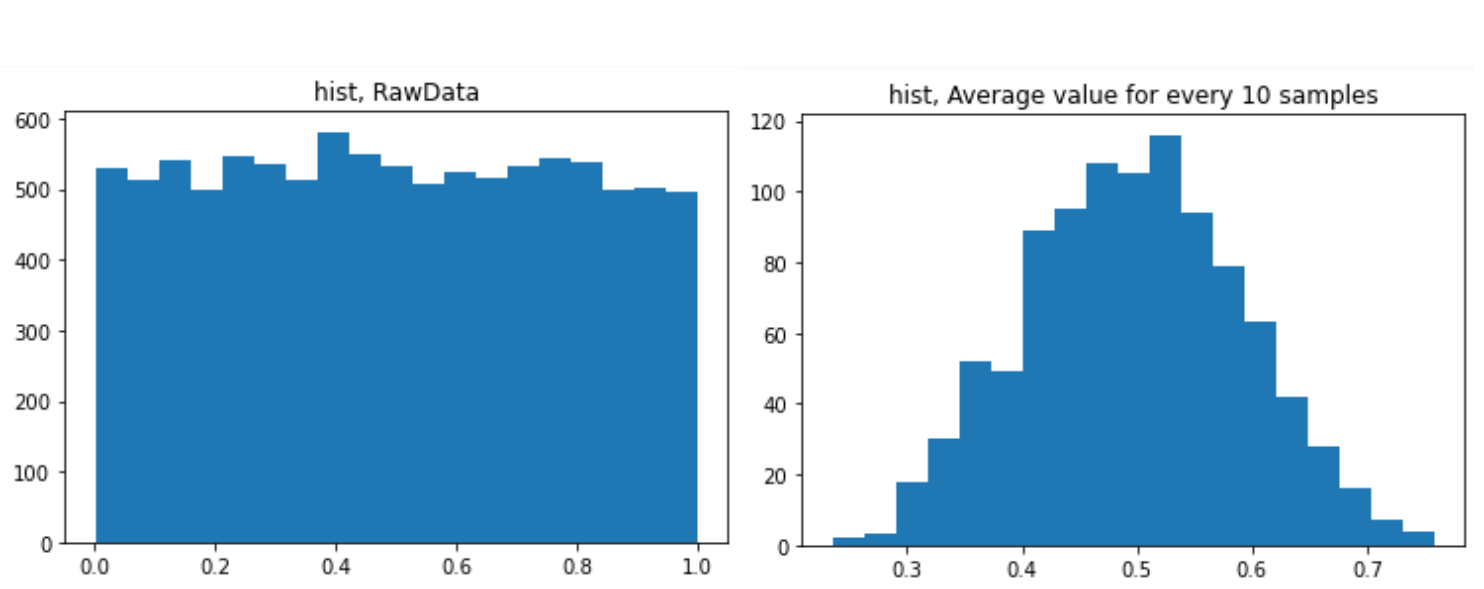
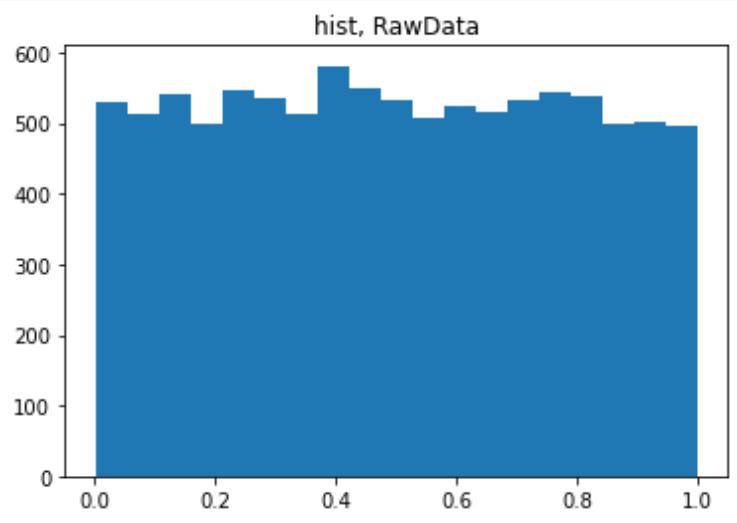
plt.title("hist, RawData")
plt.show()
# %%
dat2 = dat.reshape(1000,10)
dat2sum = dat2.mean(axis=1)
plt.figure(3)
plt.hist(dat2sum, bins=19)
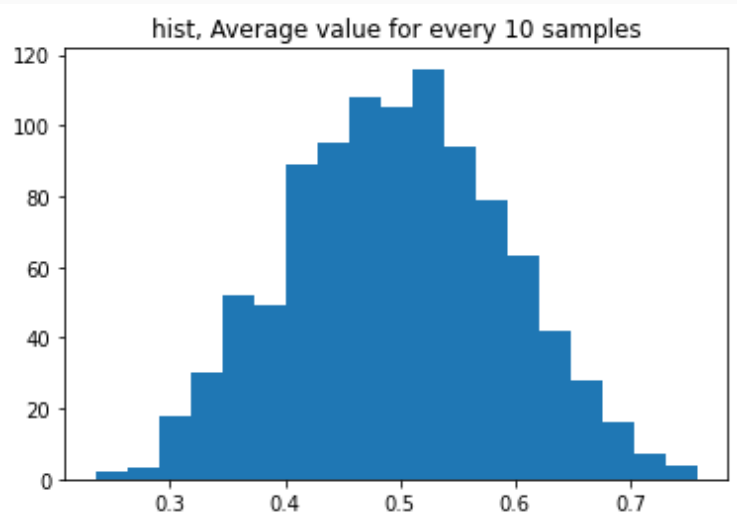
plt.title("hist, Average value for every 10 samples")
plt.show()
Numpyで集計
10000個の[0, 1.0)の「一様なはず」の乱数をnp.random.randで配列datに振り出した後、以下でヒストグラム用に集計してます。
datHist, datEdges = np.histogram(dat, bins=19)
datEdgesには19個のビンの境界を区切る20個の境界値、datHistにはビン毎の度数が格納されてます。
plt.stairs
上記で集計した結果を、plt.stairs関数に渡してみます。
plt.stairs(datHist, datEdges)
結果はこんな感じ。ヒストグラムの「上面だけ階段状につなげたグラフ」が現れます。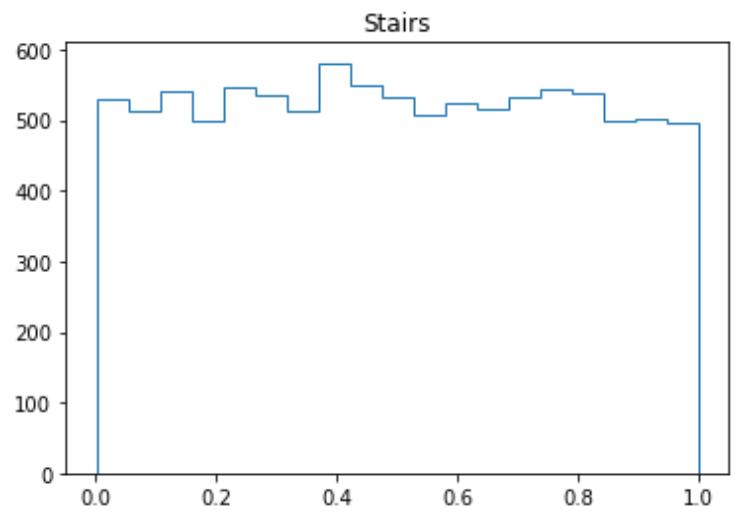
plt.hist
上記で集計した結果を、plt.hist関数に渡せば、もっとフツーのヒストグラムな感じになります。
plt.hist(datEdges[:-1], datEdges, weights=datHist)
中心極限定理
扱っているデータは一様な筈の乱数なので、多少の凸凹ありますが、平で見栄えがイマイチです。そこでトートツに中心極限定理をつかって「正規分布」にお出まし願おうと思います。計算はこんだけ。
dat2 = dat.reshape(1000,10) dat2sum = dat2.mean(axis=1)
中心極限定理を忘れているコのために、Googleの生成AI、Gemini様の解説を以下に。
さて上記で計算した平均値についてヒストグラムを描いてもらうには以下のようにできます。
plt.hist(dat2sum, bins=19)
おっと、Numpyの集計関数とか呼び出してないじゃん。でも大丈夫、そういう場合、Matplotlibの内部でよろしくやってくれるみたい。便利ね。
正規分布がまろび出てきている感がアリアリ。ホントか?