「サイエンティフィックPythonのための」IDE、Spyder上にてScientific Python Lecturesの実習中。前回はSciPyを使ってMatlab形式のバイナリ入出力をScilabとの間で確認。今回は「特殊関数」です。代表選手ということでガンマ関数をご指名。ホンワカしたグラフを描いてみます。
※「 ソフトな忘却力」投稿順 Index はこちら
※Scientific Python Lectures様のコースは例題だけでなく、エクササイズなども充実、それを全部順番に解いていったら必ずや立派な人になれるだろ~とは思います。でも量が多過ぎて死ぬまでに終わらない老い先短い年寄デス。前回から「Chapter 5 SciPy : high-level scientific computing」に入ってます。
Special functions
今回練習するのは、レクチャの「5.2 Special functions: scipy.special」です。レクチャでは以下で練習のガンマ関数を含むいくつかの関数を使っていろいろ計算しているのですが、勝手なことやってる当方ではガンマ関数のホンワカしたプロットやって通り過ぎるつもりです。なお、以下のURLで「特殊関数ども」を一覧することが可能です。
https://docs.scipy.org/doc/scipy/reference/special.html
主だった「特殊関数」にくわえ、各特殊関数の一族郎党、眷属どもも網羅している感じで名簿は充実しております。最初はちょっと統計向きの関数でも触ってお茶を濁そうかとも思ったのですが、統計関数についてはまた別のカテゴリでも登場するみたい。今回は遠慮ってことで。
そこで「特殊関数」の代表選手ということで勝手に選ばせていただいたのが、ガンマ関数です。1日前の別件シリーズの「超越関数」の説明でチラリとその名がでていました。忘却力の老人がその名をまだ覚えていた、という理由です。
さて今回「特殊関数」について調べている過程で、各種特殊関数の解説とともに
美麗なグラフ多数
を公開されているサイトがあることに気づきました。真に偉大です。「特殊関数グラフィクスライブラリー」様です。ガンマ関数の解説も、グラフなどもそちらを参照していだだくのがよろしいかと。他にも膨大なグラフあり、眺めていると時が経つのを忘れます。
念のため、以下にガンマ関数、書き添えておきます。
\( \Gamma ( x ) = \int_{0}^{\infty} t^{x-1} e^{-t} dt \)
なお、x は 0, -1, -2, …を除く、ということみたいです。
SciPy使った練習プログラム
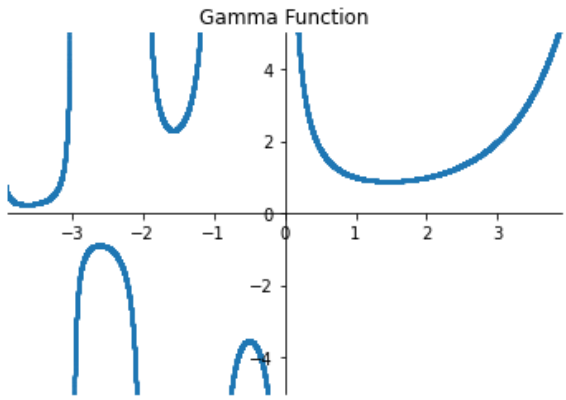
ガンマ関数は途中「切れてる」部分がある上に、一気に巨大な数へと駆け上がるのでMatplotlib素人老人は、ホンワカしたプロットするのでやっとです。こんな感じ。
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
"""
Created on Thr Jun 12 2025
@author: jhalfmoon
Gamma Function plot sample
"""
import numpy as np
import matplotlib.pyplot as plt
import scipy as sp
def main():
x = np.arange(-4.01, 5.01, 0.00011, dtype=np.double)
y = sp.special.gamma(x)
plt.scatter(x, y, s=1.0)
plt.xlim(-3.9, 3.9)
plt.ylim(-5, 5)
ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.spines['bottom'].set_position(('data',0))
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data',0))
plt.title("Gamma Function")
plt.show()
if __name__ == '__main__':
main()
なんとか雰囲気は出てるか?ホントか?