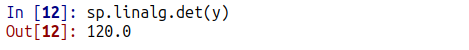「サイエンティフィックPythonのための」IDE、Spyder上にてScientific Python Lecturesの実習中。前回はSciPyの「特殊関数」でした。今回は「線形代数」です。まともにやったら分量多過ぎるので、大抵のことは皆出来る関数がある筈、ということで僅かに触ってお茶を濁す所存。
※「 ソフトな忘却力」投稿順 Index はこちら
※Scientific Python Lectures様のコースは例題だけでなく、エクササイズなども充実、それを全部順番に解いていったら必ずや立派な人になれるだろ～とは思います。でも量が多過ぎて死ぬまでに終わらない老い先短い年寄なので、適当に勝手に練習してお茶を濁してます。今回は、「5.3 Linear algebra operations: scipy.linalg」です。
Liear algebra (scipy.linalg)
Scipyの線形代数のレファレンス・ページが以下に
https://docs.scipy.org/doc/scipy/reference/linalg.html
拝見するに、実は NumPy のLinear algebraの関数を中で使役していることもままあるみたいです。NumPyの線形代数のページが以下に。
https://numpy.org/doc/stable/reference/routines.linalg.html
それどころか、どちらも底の方では「泣く子も黙る」BLASとかLAPACKとかを呼び出しているみたい。まあ、お任せしておけば性能は問題ない？
そんな線形代数を練習するのに最低覚えておくべきこと２つ。
まずは「@」です。NumPyの行列積の意味の演算子となります。
もう一つが「numpy.allclose」関数です。２つの行列の各要素が許容範囲内ならばTrueを返してくれる関数です。デフォルトでは
-
- rtol（相対差) 1e-5
- atol（絶対差) 1e-8
が許容範囲みたいです。解説ページは以下にあります。
https://numpy.org/doc/stable/reference/generated/numpy.allclose.html
今回、僅かに練習している問題は、すべて別件シリーズ「忘却の微分方程式」の過去回で練習している問題です。よって Maxima （一部、Mathematica）にて得た回答は分かっているもの。ただし、数式処理システムであるMaximaやMathematicaは、数式は数式（文字シンボル）のまま、整数は整数、有理数は分数という塩梅でご回答。浮動小数（近似値）での回答は最後の最後、どうしようもないときに限られます。一方、NumPyもSciPyも、数値的にお答えをえるための処理系です。浮動小数命っす。
逆行列
まずはNumPyとSciPyを使えるようにしておきます。
import numpy as np import scipy as sp
続いてアリガチな逆行列の計算を以下で。
x = np.array([[1, 2],[3, 4]]) xINV = sp.linalg.inv(x)
Spyderの変数エクスプローラにうつる上記の結果は以下です。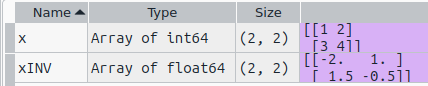
なお、この結果は別シリーズの以下記事にあります（勿論一致しているけど）
忘却の微分方程式(35) 行列と線形代数への入り口、MathematicaとMaxima
連立方程式
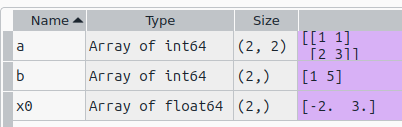
これまたアリガチな連立方程式を解いてみます。x０に解が得られている筈。
a = np.array([[1, 1],[2, 3]]) b = np.array([1, 5]) x0 = sp.linalg.solve(a, b)
結果が以下に。
@演算子とnp.allclose()関数を使って上記の検算をしてみたものが以下に。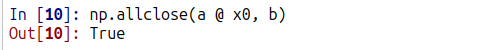
Trueでよかった。あたりまえか。
行列式
２ｘ２とか３ｘ３の行列の行列式ではちょっと楽すぎということで過去回を見直してみたら、以下の回で４ｘ４行列の行列式を求めておりました。
忘却の微分方程式(43) 反復練習７、行列式その２、Maxima
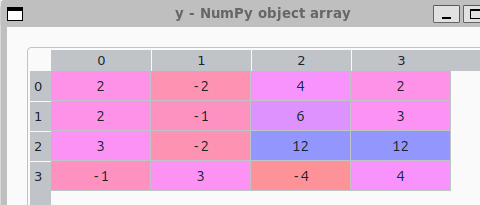
それを計算してみるのが以下に。
y = np.array([[2, -2, 4, 2],[2, -1, 6, 3],[3, -2, 12, 12],[-1, 3, -4, 4]]) sp.linalg.det(y)
行列 y はこんな感じ。
行列式を求めた結果が以下に。
固有値、固有ベクトル
比較に使った過去回が以下です。
忘却の微分方程式(48) 反復練習１２、固有値と固有ベクトル、対角化 Maxima
上記の過去回と同じ「形」で結果が欲しかったので、オプショナルなパラメータ使ったりしてみました。
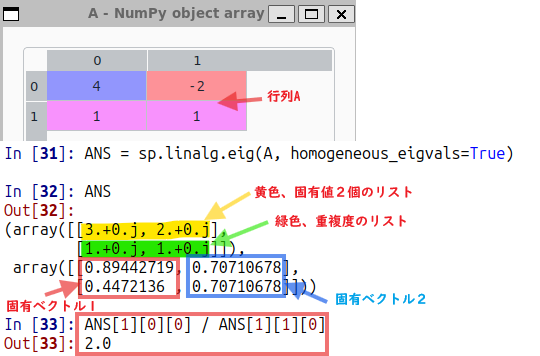
A = np.array([[4, -2],[1, 1]]) sp.linalg.eigvals(A) ANS = sp.linalg.eig(A, homogeneous_eigvals=True)
これで得た行列Aの固有値、固有ベクトルが以下に。
固有ベクトルが求まってはいるものの、浮動小数値です。Maximaの整数と分数表記とは異なります（２つのベクトルは[1, 1/2]と[1, 1]。）
まあ上記のように 0.894…は0.447…の２倍、0.707…は0.707…と同じなので、頭の中で整数、分数表記すればMaximaの結果と一致。ううむ、計算できんぜよ。。。