「サイエンティフィックPythonのための」IDE、Spyder上にてScientific Python Lecturesの実習中。前回は「補間」。今回はSciPyが ”root finding”と呼んでいる「関数の根」デス。代表的なアルゴリズムはニュートン法ね。遥か半世紀くらい前に学校でやった遠い記憶。大丈夫か？
※「 ソフトな忘却力」投稿順 Index はこちら
※Scientific Python Lectures様のコースは例題だけでなく、エクササイズなども充実、それを全部順番に解いていったら必ずや立派な人になれるだろ～と思います。でも老い先短い年寄には量が多過ぎて多分死ぬまでに終わりません。適当な練習でお茶を濁してます。今回は、「5.5 Optimization and fit: scipy.optimize」から「5.5.1 Root Finding」です。
実習する前に、お言葉「根」と「解」について気になったので調べてみました。かの結城浩先生（「数学ガール」で有名なセンセ）、が以下で書かれてました。
ううむ、勉強になるなあ。
SciPyのAPI解説ページ
以下に Optimization and root finding (scipy.optimize) へのURLを貼りました。
https://docs.scipy.org/doc/scipy/reference/optimize.html
この中に Root finding という一節があり、その中でも今回練習してみるのは Scalar functions のところです。Scalarあれば多次元空間での求解もあり、さらには「リニア・プログラミング」もここに含まれているみたい。奥が深いな Root finding。
でもま、今回は「フツーのスカラーな関数」相手です。root_scalarという関数で求めることができるみたい。何もオプション指定などしないと、みんな大好き「ニュートン法」で求めてくれるみたいっす。ただし、オプション指定すれば各種アルゴリズムが使えるようです。
ニュートン法の求根サンプル
以下はSpyder上で作成の「ちょい意地悪な」サンプルプログラムです。
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
"""
Created on Mon Jun 16 2025
@author: jhalfmoon
Scipy.optimize.root_scalar sample
"""
import sys
import scipy as sp
def f0(x):
return (x-1.0)**2
def fp(x):
return (x-1.0)**2 + sys.float_info.epsilon
def fp2(x):
return (x-1.0)**2 + 0.0001
def fn(x):
return (x-1.0)**2 - sys.float_info.epsilon
def main():
xinit = 1.1
newton0 = sp.optimize.root_scalar(f0, x0=xinit, method='newton')
print("---newton0","---"*10, "\n", newton0)
newtonp = sp.optimize.root_scalar(fp, x0=xinit, method='newton')
print("---newtonp","---"*10, "\n", newtonp)
newtonn = sp.optimize.root_scalar(fn, x0=xinit, method='newton')
print("---newtonn","---"*10, "\n", newtonn)
newtonp2 = sp.optimize.root_scalar(fp2, x0=xinit, method='newton')
print("---newtonp2","---"*10, "\n", newtonp2)
if __name__ == '__main__':
main()
ニュートン法の場合、オプショナルで対象となる関数の微分を与えられると収束が速くなるみたい（確かめてないけど。）でも今回は、比較のために「開始ポイント」を全て同じ値と指定しただけで、あとはニュートン法のデフォルトのまま計算していただいております。
ニュートン法のアルゴリズム的に「ある精度」内に落ち着いたならば根が求まったと判断して打ち切るのであろうと想像。そこで下記のような４関数を用意して実行してみました。
-
- f0、x=1.0で重根を持つ。負の値はとらないのよ。
- fp、x=1.0で限りなくｘ軸に近付くが、実は実根は存在しない。
- fn、x=1.0の上下かなり近くに２つの実根がある。
- fp2、x=1.0でｘ軸に近付くけれど、実根が存在しないのは多分アカラサマ。
実行結果
上記のプログラムの実行結果が以下に。
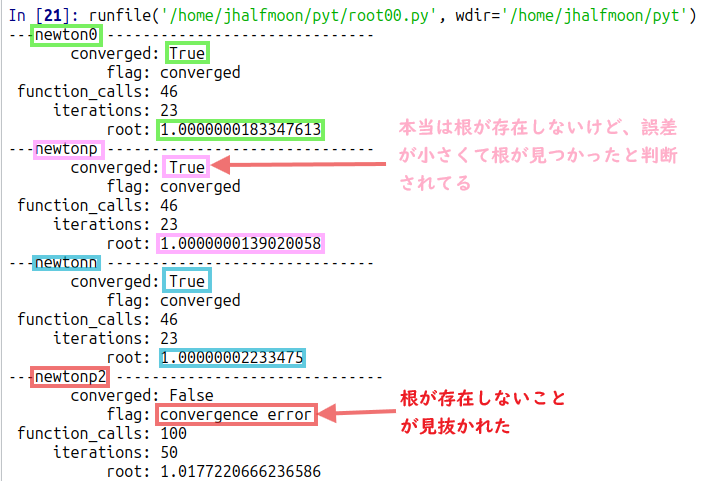重根を持つ newton0と、２根を持つnewtonnの根（そのうちの一つ）が見つかっているのは良いとして、本当は根が存在しない筈のピンクのnewtonpもサクッと根が見つかったことになっているみたいデス。convergedだと。まあ、ニュートン法のデフォルトのトレランス値がいくつか確認してないけど、newtonp関数みたいなことをすると０にタッチしていると誤解するみたい。まあ数値解だし、「限りなく近い」数字が見つかったってことで良いのか。。。
一方、アカラサマに根が存在しない筈のnewtonp2は、coverged: Flase、flag: convergence errorと判定され、「めでたく」根は存在しないことになってます。良かった。