溝口純敏様著「Maxima を使った物理数学基礎演習ノート」(以下「演習ノート」と略)を拝読中。今回は44ページ「3.3.8 Besselの微分方程式」です。「Besselの微分方程式」の解は、物理に精通された姉貴兄貴の皆さまにはお馴染みのBessel関数っす。最近別シリーズでやったばかりのΓ関数も登場の無限級数!
※「忘却の微分方程式」投稿順 index はこちら
※ MaximaおよびそのGUIであるwxMaximaの以下バージョンを使用させていただいております。
-
- wxMaxima 22.04.0
- Maxima 5.46.0(x86_64-w64-mingw32)
- SBCL 2.2.2 (SBCL = Steel Bank Common Lisp )
※Maxima を使った物理数学基礎演習ノート は以下のバージョンをダウンロードさせていただきました。
令和4 年3 月 第八回改訂
※Googleの生成AI、Gemini 2.5 Flash 様に解説をいただいた部分があります。
ベッセルの微分方程式とベッセル関数
数学素人老人は、さっさとGemini様にご説明をお願いしてしまいました。こんな感じよ。
そして、ベッセル関数として(眷属どもはいろいろあれど)以下の2つをあげておられます。
上記で、数学素人老人が黄色と緑でマーカ引きましたが、後で対応する式がでてくるので覚えておいてつかーさい。
上記のGemini様のご解説では、ベッセル関数そのものは登場しなかったので、以下、数学不得意老人がLaTeXにて記述した関数の形です。
-
- 第1種ベッセル関数
\( J_\nu (x) = \sum_{k=0}^\infty \frac{(-1)^k}{k! \Gamma(k+\nu+1)}(\frac {x}{2})^{2k+\nu} \)
-
- 第2種ベッセル関数(ノイマン関数)
\( Y_\nu (x) = \frac {J_\nu(x) cos(\nu\pi) – J_{-\nu}(x)} {sin(\nu\pi)} \)
なに気にヤバイ奴だよ、最近別シリーズでやったばかりのΓ関数まで登場する無限級数。
さて、Maxima様におかれましては 以下の日本語マニュアルページに Bessel Functions についての記述があります。
https://flex.phys.tohoku.ac.jp/texi/maxima-ja/maxima_15.html
もろもろの一族関数などは除き、「ベッセル」様のお名前を頭に頂く関数だけでも以下の4つが存在しておるみたい。
-
- bessel_j (v, z) 次数vと独立変数 zの第一種ベッセル函数
- bessel_y (v, z) 次数vと独立変数 zの第二種ベッセル函数
- bessel_i (v, z) 次数v、独立変数 zの第一種変形ベッセル函数
- bessel_k (v, z) 次数v、独立変数 zの第二種変形ベッセル函数
なお、マニュアルから1か所引用すると
計算のために無限級数は使われませんが。
ということであります。よかった。
上記のMaxima関数を列挙したのは他でもありません。Maxima様の伝家の宝刀 ode2関数に「ベッセル微分方程式」をお渡しすると、当然ながら解は上記のベッセル関数で得られるからです。実際にお願いしたところが以下に。
まずは一番上のGemini様のご説明でν(ニュー)が整数でないときと整数の時で分かれてました。それを、レクチャの記述では n と m という別な文字で宣言してます。
そうした上で、ベッセルの微分方程式を ode2関数に渡せば解が得られます。一撃よ。
もろ、解はベッセル関数デス。黄色い方が非整数、緑の方が整数デス。
ここで「演習ノート」では黄色や緑に対応する美麗なベッセル関数のグラフ登場。数学素人老人もこのグラフを描きたかったので真似してみました。こんな感じ。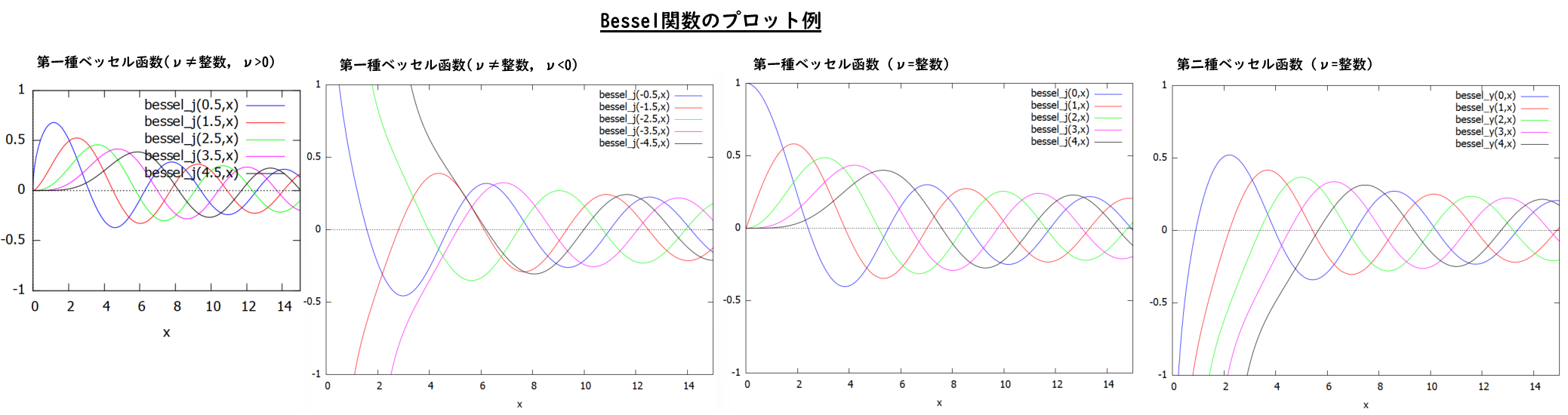
なお、毎度お世話になっております「特殊関数 グラフィックスライブラリー」様の
には、解説に加え、上記のような2次元プロットだけでなく、美麗な3Dプロット、そして「動きの分かる」動画まで掲載されています。カッケー。特殊関数、見ていると飽きんです。時間が経つのを忘れます。およよ。