「サイエンティフィックPythonのための」IDE、Spyder上にてScientific Python Lecturesの実習中。今回は別件シリーズでその姿がチラリと見えた「正規分布」と「ポアソン分布」に「二項分布」を加えた確率分布3巨頭(誰が言った?)のお姿をグラフに描く回です。違うようで似ている?なんだそれ。
※「 ソフトな忘却力」投稿順 Index はこちら
※Scientific Python Lectures様のコースは例題だけでなく、エクササイズなども充実、それを全部順番に解いていったら必ずや立派な人になれるだろ~と思います。でも老い先短い年寄には量が多過ぎて多分死ぬまでに終わりません。適当な練習でお茶を濁してます。今回は「5.6 Statistics and random numbers: scipy.stats」配下の「5.6.1 Statistical Distributions」です。
別件シリーズ
今回、5.6.1 Statistical Distributionsの練習をせねばな、と思っていたらば飛んで火にいる夏の虫、以下の別件シリーズで正規分布、ポアソン分布(たぶん切り口によっては2項分布も)がその姿をチラリと見せましたです。
データのお砂場(192) R言語、Insurance、自動車保険請求件数データ {MASS}
上記はR言語のサンプルデータセットを舐めているだけなのですが、回帰分析、lm、glm、loglmなどが登場し、そこに確率分布共が蠢いていたわけであります。そこでR言語ではなくSciPyの練習の方で確率分布どもの姿をグラフに写しとらん、と。ううむ、江戸の敵を長崎で討つ的な? 違うか?
とりあえず正規分布、二項分布、ポアソン分布を思い出す必要あり
忘却力の老人にとっては、確率分布など記憶の彼方に飛んでます。だいたい、マジメに勉強せんかったし。今更遅いよ。例によって例のごとく、Googleの生成AI、Gemini 2.5 Flash様に3種の確率分布について教えてもらいました。
そして3つの分布の関係は
ご丁寧にもGemini様は上記3つの分布の関係性についても以下のようにお教えくだすってます。やったね。
今回使用したスクリプト
上記を踏まえて、SciPy使ったPythonスクリプトを書いていきます。勿論、レクチャのExampleを参考にしつつ。なお、SciPyのAPIの解説ページは以下です。
Statistical functions (scipy.stats)
Spyder上で記述したスクリプトが以下に。
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
"""
Created on Tue Jun 24 2025
Statistical Distributions
"""
import matplotlib.pyplot as plt
import scipy as sp
def plotNorm(xloc, xsca, tstr):
dist = sp.stats.norm(loc=xloc, scale=xsca)
sample = dist.rvs(size=100000)
plt.hist(sample, bins=50, density=True, label='Normal')
plt.title(tstr)
def plotBinom(xn, xp, tstr):
rv = sp.stats.binom(xn, xp)
sample = rv.rvs(size=100000)
plt.hist(sample, bins=50, density=True, label='Binomial')
plt.title(tstr)
def plotPoisson(mu, tstr):
rv = sp.stats.poisson(mu)
sample = rv.rvs(size=100000)
plt.hist(sample, bins=50, density=True, label='Poisson')
plt.title(tstr)
def main():
plt.subplot(2,3,1)
plotNorm(0,1.0,"Normal")
plt.subplot(2,3,2)
plotBinom(100, 0.05,"Binomial p=0.05")
plt.subplot(2,3,3)
plotPoisson(0.2,"Poisson mu=0.2")
plt.subplot(2,3,4)
plotBinom(100, 0.5,"Binomial p=0.5")
plt.subplot(2,3,5)
plotBinom(100, 0.01,"Binomial p=0.01")
plt.subplot(2,3,6)
plotPoisson(10.0,"Poisson mu=10")
plt.tight_layout()
plt.show()
if __name__ == '__main__':
main()
描かれた確率分布のお姿
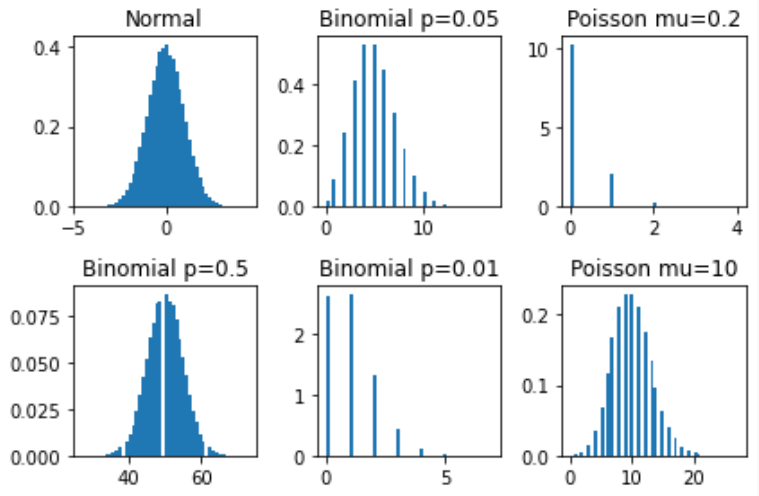
上記スクリプトで描いた分布の姿が以下に。なお、図中で使っているpとかmuとかのシンボル名はSciPyの解説ページで記述されている記号に合わせてあります。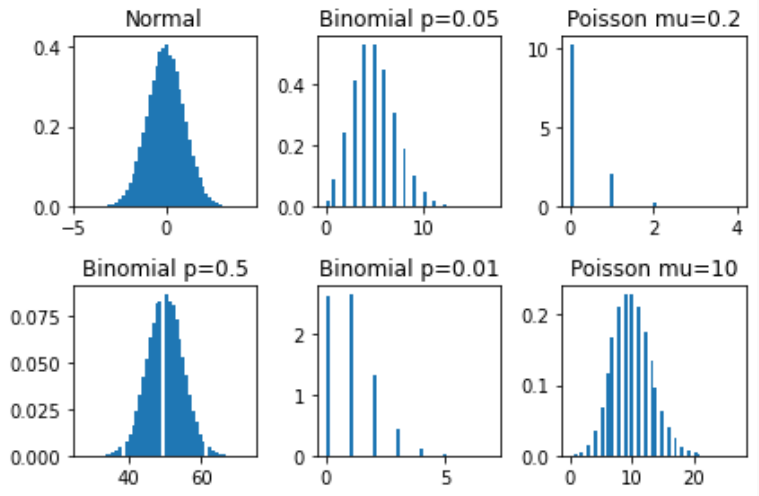
上段、左に、平均0、標準偏差1の正規分布が鎮座、その右にアリガチな形の2項分布、そしてポアソン分布がつづきます。この段を見ると3つの分布は違う印象。
しかし下段に行くと、左端の2項分布は正規分布っぽい? そして真ん中の2項分布はポアソンっぽい?さらに、右下のポアソン分布は正規分布っぽい?
まあGemini様のお教え通りなんだが。