
「サイエンティフィックPythonのための」IDE、Spyder上にてScientific Python Lecturesの実習中。前回はフィルタを作成、今回はフィルタ(LPF)に信号を通して結果を観察するの回です。コンボリューション(畳みこみ)の関数利用。同じことをやるのでScilabの関数と使い方はよう似てます。
※「 ソフトな忘却力」投稿順 Index はこちら
※Scientific Python Lectures様のコースは例題だけでなく、エクササイズなども充実、それを全部順番に解いていったら必ずや立派な人になれるだろ~と思います。でも老い先短い年寄には量が多過ぎて多分死ぬまでに終わりません。適当な練習でお茶を濁してます。今回の「お勉強」は「5.9 Signal processing: scipy.signal」です。
コンボリューション(畳み込み)
SciPyのコンボリューション関数のAPIページが以下に。
また、以下の別シリーズ回にて、Scilabの畳み込み関数を使ってみています。
手習ひデジタル信号処理(134) Scilab、conv、convol、離散一次元畳み込み
まったく同じ計算をやろうというので当然なのですが、SciPy、Scilabとも引数などよく似ています、というか同じスタイルです。信号とカーネルを組み合わせる方法を指定するオプションなどまったく同じです。
-
- full(デフォルト)
- same
- valid
上記の違いなどは上記の過去記事に図解あります。
また、「真正面から」コンボリューションを計算すると計算負荷が重くなる巨大な配列を相手にするために fftを応用したコンボリューション関数があることも同様です。
-
- Scilabでは、「真正面から」畳み込みを行うのは conv 関数、「FFT使って」高速化を試みるのが、convol 関数
- SciPyのconvolve関数では、directオプションで「真正面から」、fftオプションでは「FFT使って」となるみたいです。なお、デフォルト(autoオプション)では、配列のサイズを見計らって速そうな方を自動選択してくれるみたい。便利ね(なお、fftconvolve関数使うと常にFFT選択。)
LPFフィルタで不要な周波数をカットするスクリプト
以下では、第101回で生成した2つの正弦波波形が重なっている信号を入力として、LPFフィルタ(前回登場したfirwin関数で作成)を適用し、低い周波数(440Hz)をとりだし、高い周波数(4186Hz)を抑圧してみてます。
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
"""
Created on Tue Jul 1 2025
Modified on Jul 6 2025
@author: jhalfmoon
LPF sample
"""
import numpy as np
import matplotlib.pyplot as plt
import scipy as sp
def main():
N = 4410 # 44.1kHz * 1/10
T = 1.0 / 44410.0 # sampling interval
x = np.linspace(0.0, N*T, N, endpoint=False)
y440 = np.sin(440.0 * 2.0 * np.pi * x)
y4186 = np.sin(4186.0 * 2.0 * np.pi * x)
y = y440 + 0.1 * y4186
lpf1 = sp.signal.firwin(31, 0.05*2, pass_zero='lowpass')
ylpf = sp.signal.convolve(y, lpf1, mode='same')
yf = sp.fft.fft(y)
xf = sp.fft.fftfreq(N, T)[:N//2]
ylpfF = sp.fft.fft(ylpf)
plt.subplot(2,2,1)
plt.plot(x, y)
plt.xlim(0, 0.01)
plt.title("Signal: 440Hz + 4186Hz")
plt.subplot(2,2,2)
plt.plot(x, ylpf)
plt.xlim(0, 0.01)
plt.title("LPF result")
plt.subplot(2,2,3)
plt.semilogy(xf[1:N//2], 2.0/N * np.abs(yf[1:N//2]), '-b')
plt.title("FFT : Signal")
plt.grid()
plt.subplot(2,2,4)
plt.semilogy(xf[1:N//2], 2.0/N * np.abs(ylpfF[1:N//2]), '-b')
plt.title("FFT : Filtered")
plt.grid()
plt.tight_layout()
plt.show()
if __name__ == '__main__':
main()
スクリプトの実行結果
実行結果のグラフが以下に。上段が時間波形、下段がFFTかけた結果です。左が2種類の周波数が重なった入力信号、右がLPFかけた後の出力信号です。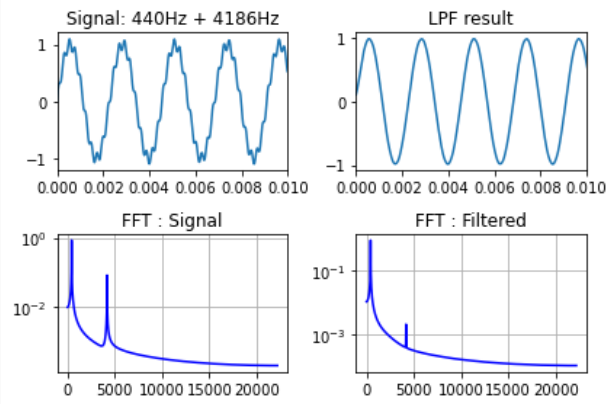
目論見どおり、低い周波数だけが取り出せている感じですわい。