
「サイエンティフィックPythonのための」IDE、Spyder上にてScientific Python Lecturesの実習中。前回はモフォロジー処理でした。今回はムツカシク言うと連結成分解析(CCA)ということみたい。画像内の「つながっている」部分を塊にして、部分ごとにラベルを付ける処理っす。
※「 ソフトな忘却力」投稿順 Index はこちら
※Scientific Python Lectures様のコースは例題だけでなく、エクササイズなども充実、それを全部順番に解いていったら必ずや立派な人になれるだろ~と思います。でも老い先短い年寄には量が多過ぎて多分死ぬまでに終わりません。適当な練習でお茶を濁してます。今回の「お勉強」は「5.10 Image manipulation: scipy.ndimage」の「5.10.4 Connected components and measurements on images」です。
画像のセグメンテーションと連結成分解析
ここで言う「セグメンテーション」は、画像内のオブジェクトと背景を区別し、オブジェクト部分を取り出す処理です。また、連結成分解析(Connected Component Analysis)は、連結した画素群(セグメンテーションで区別された部分など)について、ユニークなラベル(数値)を与える処理です。レクチャでは三角関数使って「算術的に」生成したサンプル画像を使って処理しているのだけれども、イマイチ泥臭さに欠けます。当方では以下の10円玉画像を例題としてみます。
茶っぽく見える10円玉部分を緑の背景に対して画素グループ「オブジェクト」としてラベル付けを行いたいと思います。
ナケナシの10円玉3個也、を使ったのは、別シリーズの以下の過去回のScilabのIPCVの例題で「コインを使ったサンプル画像で似た操作」をしたことがあるからです。
手習ひデジタル信号処理(141) Scilab、{IPCV}、モルフォロジー処理その2
今回はそのときの操作に相当する処理を、SciPyの関数でやってみようという趣向です。処理のステップはだいたい以下のとおり。
-
- 元画像を読み込む
- 読み込んだ画像を単純な2次元画像(深さ1、グレースケール)につぶす
- 上記画像をスレッショルド処理して二値化
- 2値化画像にモフォロジー処理を加えてオブジェクトを整形
- 上記の整形結果をラベル付け
- 各ラベル領域毎の特徴を数値として出力
使用したスクリプト
上記の処理ステップをSciPyの関数使って書いてみたものが以下のスクリプトです。なお、matplotlibのimread関数で読み込んだ結果の画像の配列の次元は3次元になるようです。最初の2つは平面内の次元ですが、色方向に深さの次元があります。深さはRGBαで4ということみたい。このRGBα(αはアルファチャンネル)を「押しつぶして」1個の数字にしてしまえば、単純な2次元の配列にできるっと。ここは前回もやったとおり。
またオブジェクトを整形するためのモフォロジー処理は、膨張(あるいは黒白反転しているならば収縮)するのが定番(別シリーズの過去回では「膨張」つかっていた)じゃないかと思います。しかし、今回は前回、膨張、収縮は練習しなかったという理由で closing 処理でやってみました。やればできるもんだね。
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
"""
Created on Fri Jul 11 2025
@author: jhalfmoon
Mask, Label Operations sample
"""
import numpy as np
import matplotlib.pyplot as plt
import scipy as sp
def plotBin(fig, title):
plt.imshow(fig, cmap="gray")
plt.title(title)
def main():
img = plt.imread('Coins3B.png')
imgGray = np.mean(img, axis=2)
threshold = 0.69
imgWork = (imgGray < threshold).astype(int)
mask = sp.ndimage.grey_closing(imgWork, size=(10,10))
labels, nb = sp.ndimage.label(mask)
print("# of labels:", nb)
areas = sp.ndimage.sum(mask, labels, range(1, labels.max()+1))
print("areas: ",areas)
maxima = sp.ndimage.maximum(imgGray, labels, range(1, labels.max()+1))
print("maxima: ",maxima)
plt.figure(figsize=[12.8,4.8])
plt.subplot(161)
plt.imshow(img)
plt.title("Original")
plt.subplot(162)
plt.imshow(imgGray)
plt.title("Converted: 2D array")
plt.subplot(163)
plotBin(imgWork, "binary")
plt.subplot(164)
plotBin(mask, "Mask: after closing")
plt.subplot(165)
plt.imshow(labels)
plt.title("Labels")
plt.tight_layout()
plt.show()
if __name__ == '__main__':
main()
スクリプトの実行結果
まずは処理の各段階でどのような画像が得られているか左から右に並べたもの。
左のオリジナルのカラー画像から、右端のラベル画像(ラベル値毎に色がついている)に向かって処理されてます。
そして数値データとして出力されているラベル画像の特徴が以下に、
10円玉は3個(右下の1個は端っこにかかっており、3分の1くらいの面積のみ見えている)あり、それに該当するのが上記のエリアの黄色マーカ部分です。なお、maximaというベクトルにその領域内の信号値の最大が与えられてます。その後に「小さい」ラベルが2つ(当然10円玉ではない)もあるみたい。右端のラベル画像を拡大して人力で矢印描いたものが以下に。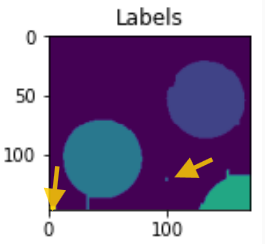
矢印の先にちょこっと見えているボッチがそれです。こいつらはゴミだ、ということで深く追求なし。いいのかそういうことで。