
「サイエンティフィックPythonのための」IDE、Spyder上にてScientific Python Lecturesの実習中。前回はイテレータ。ということで今回はジェネレータ(Generator)です。まあいつも知らず知らずにお世話になっているけれども、今回は明示的にジェネレータ作ってみるということで。
※「 ソフトな忘却力」投稿順 Index はこちら
※Scientific Python Lectures様のコースは例題だけでなく、エクササイズなども充実、それを全部順番に解いていったら必ずや立派な人になれるだろ~と思います。でも老い先短い年寄には量が多過ぎて多分死ぬまでに終わりません。適当な練習でお茶を濁してます。今回は「7. Advanced Python Constructs」の「7.1.2 Generator expressions」です。
ジェネレータ
以下にGoogleの生成AI、Gemini 2.5 Flash様にPythonのジェネレータについて説明していだたものを掲げます。
レクチャの7.1.2 Generator expressions では、そのタイトルどおり上記の「ジェネレータ式」を使って値を「ジェネレーション」する例のみ取り扱ってます。Pythonでお馴染みの「リスト内包表記」などで呼び出されるジェネレーターどもです。レクチャの7.1.2では yield つかってジェネレータを作ることをしていなかったので、御勝手なお惚け老人は yield つかってみることにいたします。
ポアソン分布
さて、yield使って記述するものを考えました。前回イテレータの回では、無限につづく数列であるフィボナッチ数列を例に使ってしまいました。今となってはジェネレータの例でやった方が良かったか?そんなこと思っても後の祭りです。
そこで、呼び出されるとパラメータ指定済のポアソン分布に従った乱数を一つ返すジェネレータ関数を作ってみることにいたしました。ただね、Numpy.randomが備える、poisson関数にはsizeというパラメータもあり、ご要望に応じて好きなだけの個数の乱数リストを返すことが可能。 わざわざ自前のジェネレータ関数を作る必要もリスト内包する必要もないです。まあ、練習ってことで。
念のため、ポアソン分布についてもGemini様にご説明いただきましたぞ。
ジェネレータを使ったポアソン分布乱数の「殊更な」実装
実際にポアソン分布での乱数生成は、Numpy.random.poissonを呼び出してます。その上に被せるジェネレータ関数としてPoissonGenという関数を用意しました。乱数の種(seed)と、平均値ラムダ(λ)を引数としてとるオブジェクトを返すものです。このオブジェクトを呼び出す度に、毎回ポアソン分布に従う乱数が1個振り出されます。
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
"""
Created on Fri Jul 18 2025
@author: jhalfmoon
Poisson distribution random number generator
"""
import numpy as np
import matplotlib.pyplot as plt
def PoissonGen(seed, lm):
rng = np.random.default_rng(seed)
while True:
yield rng.poisson(lam=lm) #No size parameter
def main():
PoissonObj = PoissonGen(12345, 2)
lis = [next(PoissonObj) for _i in range(100000)]
plt.hist(lis, bins=10, range=(0,10), density=True)
plt.title('Poisson distribution')
plt.show()
if __name__ == '__main__':
main()
ジェネレータを使ってみた結果
かなり「わざとらしい」上の書き方で100000回ジェネレータを呼び出して、その結果をリストとして返し、それをヒストグラムに直して描いたものが以下に。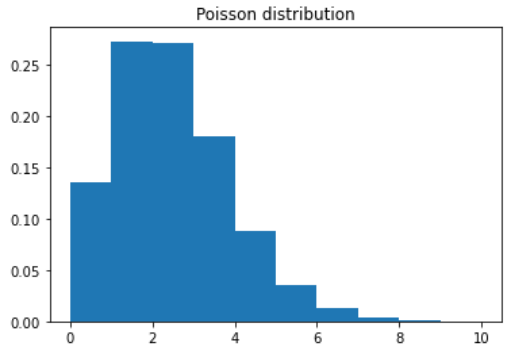
縦軸はデンシティです。全体1としたときの比率ね。平均値2のポアソン分布をお願いしたので、2がピークになっている感じです。まあ、だいたいポアソン分布の形じゃなかろうか?いい加減だが、いつもの通り。