信号処理素人老人がScilabの「信号処理のデモ」からカテゴリ脱出。前回はローレンツ・アトラクタにSUNDIALSのArkodeソルバを適用しました。今回はcvodeソルバ適用ですが脇役。モデルパラメータを推定の巻です。ターゲットのモデルはSIRモデルとな。感染症の一番シンプルなモデルね。昔やったような気がするんだが。
※「手習ひデジタル信号処理」投稿順 Indexはこちら
※Windows11上の Scilab2024.0.0を使用させていただいております。(Scilabについては御本家 Scilab 様へ)
SIRモデル
いくつかの簡単な仮定を置いた上で、S(Susceptible)感染する可能性がある人、I(Infected)感染者、R(Recovered)回復者(またはRemoved、隔離者)の3グループ間の増減の関係を表した感染症の流行のモデルです。
\(\frac {dS(t)} {dt} = -βS(t)I(t)\)
\(\frac {dI(t)} {dt} = βS(t)I(t)-γI(t)\)
\(\frac {dR(t)} {dt} = γI(t)\)
ここで、パラメータβとγは以下です。
-
- β、感染率
- γ、回復率
SIRモデルが仮定している前提条件についてGoogleの生成AI、Gemini 2.5 Flash様にお教えいただきましたぞ。
SIRモデルについては、コロナの時期に、以下の別件シリーズで「練習」してみたことがあります。この時使用したのが、Scilab/Xcosでした。
上記は、全てパラメータも初期値も分かっていて(外から与えた)、それに基づいて増減を計算するものでした。
SUNDIALS、Parameter identification in ODEデモ
さて、今回「鑑賞」してみるSUNDIALSのデモは Parameter identification in ODEというものです。高機能で高速な「ソルバ・スイート」のSUNDIALSをわざわざ使うのですから、過去回のように真っすぐ計算しておしまい、などということはありますまい。
デモのスクリプトは、以下の名前のファイルであります。
demo_sir_ident.sce
その目的は以下引用文のとおりです。
identification of initial conditions and parameters of SIR epidemiologic model
常微分方程式系であり、ソルバとしてはcvode、SUNDIALS ordinary differential equation solverを使うようになっています。しかし、
-
- データとして時間と感染者数のデータが与えられる(スクリプトの中にデータ配列を含む)
- 上記データにフィットするパラメータと初期値をoptim()関数で推定する
という点でなんだか「実用的」な感じです。
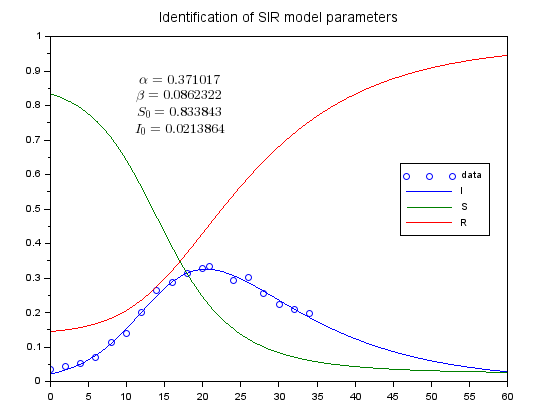
〇が打たれているのがデータ点で、上の方に数値で書かれてるのが、推定したモデルのパラメータと初期値です。一般に、SIRモデルのパラメータは、βとγで表すのではないかと思われますが、このデモ・スクリプトでは以下のシンボル使っているみたいっす。
-
- α、感染率(普通はβだけれども)
- β、回復率(普通はγだけれども)
線で描かれているのが、推定したモデルのパラメータと初期値から「描かれた」グラフです。いい感じで推定できているんでないかい?