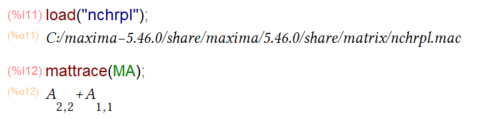溝口純敏様著「Maxima を使った物理数学基礎演習ノート」（以下「演習ノート」と略）を拝読中。前回は「行列」の生成でした。今回は「演算」です。といってもお惚け老人は超基本的なところを触るだけでお茶を濁してマス。相当前の過去回の間延びした復習みたいなもんか？そんなわけで演習流させていただきます。手抜きだな。
※「忘却の微分方程式」投稿順 index はこちら
※ MaximaおよびそのGUIであるwxMaximaの以下バージョンを使用させていただいております。
-
- wxMaxima 22.04.0
- Maxima 5.46.0(x86_64-w64-mingw32)
- SBCL 2.2.2 (SBCL = Steel Bank Common Lisp )
※Maxima を使った物理数学基礎演習ノート は以下のバージョンをダウンロードさせていただきました。
令和4 年3 月 第八回改訂
今回は「演習ノート」では、「4.2 行列とテンソル」の「4.2.2 行列の演算」のあたりデス。実際には演算規則などかなりお教えいただいてるのだけれども、以下はトッテモ手抜き。
行列の和
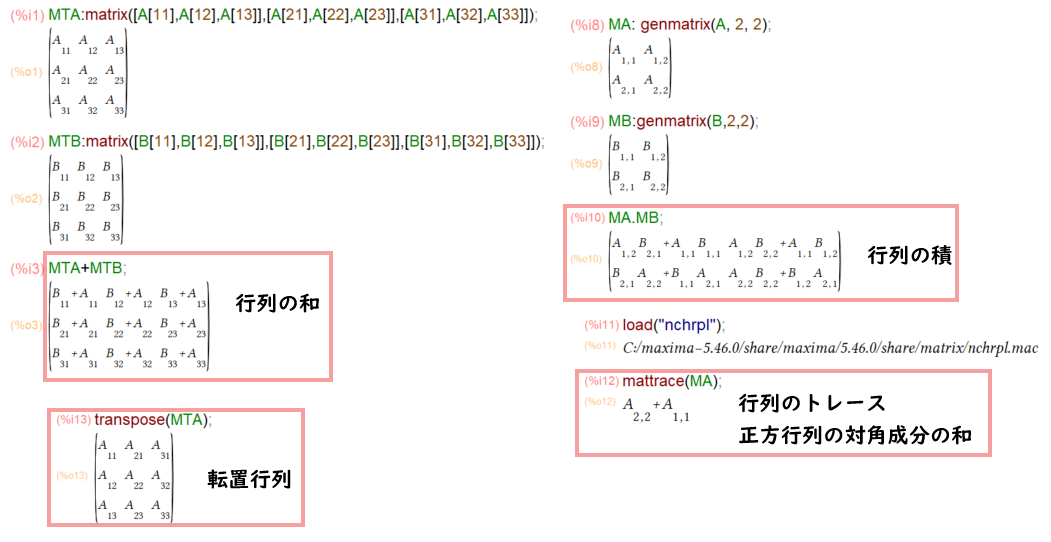
２個の３ｘ３行列ＭＴＡとＭＴＢを成分から定義して、和を求めるのが以下に。
MTA:matrix([A[11],A[12],A[13]],[A[21],A[22],A[23]],[A[31],A[32],A[33]]); MTB:matrix([B[11],B[12],B[13]],[B[21],B[22],B[23]],[B[31],B[32],B[33]]); MTA+MTB;
Maxima上での実行結果が以下に。
行列の積
今度は genmatrix使って添え字から２個の２ｘ２行列、ＭＡとＭＢを生成して積を求めるもの。
MA:genmatrix(A,2,2); MB:genmatrix(B,2,2); MA.MB;
Maxima上での実行結果が以下に。
行列のトレース
お次は、行列のトレース（正方行列の対角成分の和）です。「演習ノート」では正面から計算して演算規則を確かめてます。
「素のMaxima」は行列のトレースを直接求める関数は含んでないようなので、nchrplというパッケージ（当方では、デフォルトで付属してました）をロードし、上のMA行列のトレースを求めてみたのが以下に。
load("nchrpl");
mattrace(MA);
Maxima上での実行結果が以下に。
どうも、nchrplというパッケージは、泣く子も黙るMACSYMA様のCHARPOLYという関数と同等のもの（ncharpoly)をMaxima上でも欲しいということで設けられたパッケージみたい。mattraceはncharpolyの中で使われているので定義されているみたい。知らんけど。
転置行列
過去回で何度となく転置してますが、復習ということで。
transpose(MTA);
Maxima上での実行結果が以下に。
何時も？な手抜き回の終わり。大丈夫か。